ЬтФПФкШн
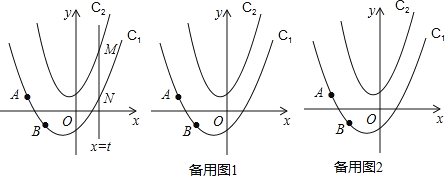
ЁОЬтФПЁПдФЖСЯТСаВФСЯЃЌВЂЭъГЩШЮЮё. Ш§НЧаЮЕФЭтаФЖЈвхЃКШ§НЧаЮШ§БпЕФДЙжБЦНЗжЯпЯрНЛгквЛЕуЃЌетИіЕуНазіШ§НЧаЮЕФЭтаФЃЌШчЭМ1ЃЌжБЯп![]() ЗжБ№ЪЧБп
ЗжБ№ЪЧБп![]() ЕФДЙжБЦНЗжЯп.
ЕФДЙжБЦНЗжЯп.
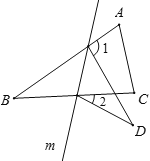
ЧѓжЄЃКжБЯп![]() ЯрНЛгквЛЕу.
ЯрНЛгквЛЕу.
жЄУїЃКШчЭМ2ЃЌЩш![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌЗжБ№СЌНг
ЃЌЗжБ№СЌНг![]()
Ёп![]() ЪЧ
ЪЧ![]() ЕФДЙжБЦНЗжЯпЃЌ
ЕФДЙжБЦНЗжЯпЃЌ
Ёр![]() ЃЌЃЈвРОн1ЃЉ
ЃЌЃЈвРОн1ЃЉ
Ёп![]() ЪЧ
ЪЧ![]() ЕФДЙжБЦНЗжЯпЃЌ
ЕФДЙжБЦНЗжЯпЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌЃЈвРОн2ЃЉ
ЃЌЃЈвРОн2ЃЉ
Ёп![]() ЪЧ
ЪЧ![]() ЕФДЙжБЦНЗжЯпЃЌ
ЕФДЙжБЦНЗжЯпЃЌ
ЁрЕу![]() дк
дк![]() ЩЯЃЌЃЈвРОн3ЃЉ
ЩЯЃЌЃЈвРОн3ЃЉ
ЁржБЯп![]() ЯрНЛгквЛЕу.
ЯрНЛгквЛЕу.
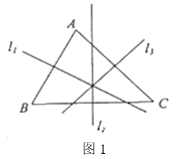
ЃЈ1ЃЉЩЯЪіжЄУїЙ§ГЬжаЕФЁАвРОн1ЁБЁАвРОн2ЁБЁАвРОн3ЁБЗжБ№жИЪВУДЃП
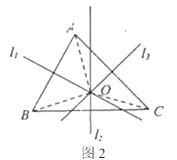
ЃЈ2ЃЉШчЭМ3ЃЌжБЯп![]() ЗжБ№ЪЧ
ЗжБ№ЪЧ![]() ЕФДЙжБЦНЗжЯпЃЌжБЯп
ЕФДЙжБЦНЗжЯпЃЌжБЯп![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌЕу
ЃЌЕу![]() ЪЧ
ЪЧ![]() ЕФЭтаФЃЌ
ЕФЭтаФЃЌ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌЗжБ№СЌНг
ЃЌЗжБ№СЌНг![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() . Шє
. Шє![]() ЃЌ
ЃЌ![]() ЕФжмГЄЮЊ
ЕФжмГЄЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжмГЄ.
ЕФжмГЄ.
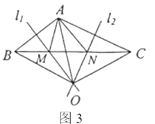
ЁОД№АИЁПЃЈ1ЃЉвРОн1ЃКЯпЖЮДЙжБЦНЗжЯпЩЯЕФЕугыетЬѕЯпЖЮСНИіЖЫЕуЕФОрРыЯрЕШЃЛвРОн2ЃКЕШСПДњЛЛЃЛвРОн3ЃКгывЛЬѕЯпЖЮСНИіЖЫЕуОрРыЯрЕШЕФЕуЃЌдкетЬѕЯпЖЮЕФДЙжБЦНЗжЯпЩЯЃЛЃЈ2ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЭЦРэЙ§ГЬКЭДЙжБЦНЗжЯпЕФаджЪКЭХаЖЈЕУГіД№АИ
ЃЈ2ЃЉИљОнДЙжБЦНЗжЯпЕФаджЪЕУГі![]() ЕФжмГЄ=BCКЭ
ЕФжмГЄ=BCКЭ![]() ЃЌдйИљОн
ЃЌдйИљОн![]() ЕФжмГЄМДПЩЕУГіД№АИ
ЕФжмГЄМДПЩЕУГіД№АИ
ЃЈ1ЃЉвРОн1ЃКЯпЖЮДЙжБЦНЗжЯпЩЯЕФЕугыетЬѕЯпЖЮСНИіЖЫЕуЕФОрРыЯрЕШ
вРОн2ЃКЕШСПДњЛЛ
вРОн3ЃКгывЛЬѕЯпЖЮСНИіЖЫЕуОрРыЯрЕШЕФЕуЃЌдкетЬѕЯпЖЮЕФДЙжБЦНЗжЯпЩЯ
ЃЈ2ЃЉНтЃКЁпжБЯп![]() ЪЧ
ЪЧ![]() ЕФЕФДЙжБЦНЗжЯп
ЕФЕФДЙжБЦНЗжЯп
Ёр![]() ЃЌ
ЃЌ
ЁпжБЯп![]() ЪЧ
ЪЧ![]() ЕФЕФДЙжБЦНЗжЯп
ЕФЕФДЙжБЦНЗжЯп
Ёр![]()
Ёр![]() ЃЌ
ЃЌ![]() ЕФжмГЄ
ЕФжмГЄ![]() ЃЌ
ЃЌ
Ёп![]() ЕФжмГЄЮЊ
ЕФжмГЄЮЊ![]()
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЕФжмГЄЮЊ
ЕФжмГЄЮЊ![]() .
.