ЬтФПФкШн
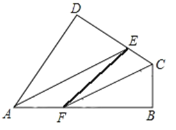
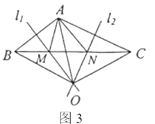
ЁОЬтФПЁПШчЭМ1ЃЌЁїABCгыЁїCDEЖМЪЧЕШбќжБНЧШ§НЧаЮЃЌжБНЧБпACЃЌCDдкЭЌвЛЬѕжБЯпЩЯЃЌЕуMЁЂNЗжБ№ЪЧаББпABЁЂDEЕФжаЕуЃЌЕуPЮЊADЕФжаЕуЃЌСЌНгAEЃЌBDЃЌPMЃЌPNЃЌMNЃЎ
ЃЈ1ЃЉЙлВьВТЯыЃК
ЭМ1жаЃЌPMгыPNЕФЪ§СПЙиЯЕЪЧЁЁ ЁЁЃЌЮЛжУЙиЯЕЪЧЁЁ ЁЁЃЎ
ЃЈ2ЃЉЬНОПжЄУїЃК
НЋЭМ1жаЕФЁїCDEШЦзХЕуCЫГЪБеыа§зЊІСЃЈ0ЁуЃМІСЃМ90ЁуЃЉЃЌЕУЕНЭМ2ЃЌAEгыMPЁЂBDЗжБ№НЛгкЕуGЁЂHЃЌХаЖЯЁїPMNЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЭиеЙбгЩьЃК
АбЁїCDEШЦЕуCШЮвта§зЊЃЌШєAC=4ЃЌCD=2ЃЌЧыжБНгаДГіЁїPMNУцЛ§ЕФзюДѓжЕЃЎ

ЁОД№АИЁПЃЈ1ЃЉPM=PNЃЌPMЁЭPNЃЈ2ЃЉМћНтЮіЃЈ3ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЕШбќжБНЧШ§НЧаЮЕФаджЪвзжЄЁїACEЁеЁїBCDЃЌгЩДЫПЩЕУAE=BDЃЌдйИљОнШ§НЧаЮжаЮЛЯпЖЈРэМДПЩЕУЕНPM=PNЃЌгЩЦНааЯпЕФаджЪПЩЕУPMЁЭPNЃЛ
ЃЈ2ЃЉЃЈ1ЃЉжаЕФНсТлШдОЩГЩСЂЃЌгЩЃЈ1ЃЉжаЕФжЄУїЫМТЗМДПЩжЄУїЃЛ
ЃЈ3ЃЉгЩЃЈ2ЃЉПЩжЊЁїPMNЪЧЕШбќжБНЧШ§НЧаЮЃЌPM=![]() BDЃЌЭЦГіЕБBDЕФжЕзюДѓЪБЃЌPMЕФжЕзюДѓЃЌЁїPMNЕФУцЛ§зюДѓЃЌЭЦГіЕБBЁЂCЁЂDЙВЯпЪБЃЌBDЕФзюДѓжЕ=BC+CD=6ЃЌгЩДЫМДПЩНтОіЮЪЬтЃЛ
BDЃЌЭЦГіЕБBDЕФжЕзюДѓЪБЃЌPMЕФжЕзюДѓЃЌЁїPMNЕФУцЛ§зюДѓЃЌЭЦГіЕБBЁЂCЁЂDЙВЯпЪБЃЌBDЕФзюДѓжЕ=BC+CD=6ЃЌгЩДЫМДПЩНтОіЮЪЬтЃЛ
ЃЈ1ЃЉPM=PNЃЌPMЁЭPNЃЌРэгЩШчЯТЃК
бгГЄAEНЛBDгкOЃЌ
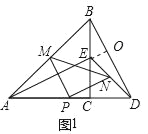
ЁпЁїACBКЭЁїECDЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрAC=BCЃЌEC=CDЃЌЁЯACB=ЁЯECD=90ЁуЃЎ
дкЁїACEКЭЁїBCDжа
 ЃЌ
ЃЌ
ЁрЁїACEЁеЁїBCDЃЈSASЃЉЃЌ
ЁрAE=BDЃЌЁЯEAC=ЁЯCBDЃЌ
ЁпЁЯEAC+ЁЯAEC=90ЁуЃЌЁЯAEC=ЁЯBEOЃЌ
ЁрЁЯCBD+ЁЯBEO=90ЁуЃЌ
ЁрЁЯBOE=90ЁуЃЌМДAEЁЭBDЃЌ
ЁпЕуMЁЂNЗжБ№ЪЧаББпABЁЂDEЕФжаЕуЃЌЕуPЮЊADЕФжаЕуЃЌ
ЁрPM=![]() BDЃЌPN=
BDЃЌPN=![]() AEЃЌ
AEЃЌ
ЁрPM=PMЃЌ
ЁпPMЁЮBDЃЌPNЁЮAEЃЌAEЁЭBDЃЌ
ЁрЁЯNPD=ЁЯEACЃЌЁЯMPA=ЁЯBDCЃЌЁЯEAC+ЁЯBDC=90ЁуЃЌ
ЁрЁЯMPA+ЁЯNPC=90ЁуЃЌ
ЁрЁЯMPN=90ЁуЃЌ
МДPMЁЭPNЃЌ
ЙЪД№АИЪЧЃКPM=PNЃЌPMЁЭPNЃЛ
ЃЈ2ЃЉШчЭМЂкжаЃЌЩшAEНЛBCгкOЃЌ
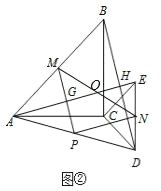
ЁпЁїACBКЭЁїECDЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрAC=BCЃЌEC=CDЃЌ
ЁЯACB=ЁЯECD=90ЁуЃЌ
ЁрЁЯACB+ЁЯBCE=ЁЯECD+ЁЯBCEЃЌ
ЁрЁЯACE=ЁЯBCDЃЌ
ЁрЁїACEЁеЁїBCDЃЌ
ЁрAE=BDЃЌЁЯCAE=ЁЯCBDЃЌ
гжЁпЁЯAOC=ЁЯBOEЃЌ
ЁЯCAE=ЁЯCBDЃЌ
ЁрЁЯBHO=ЁЯACO=90ЁуЃЌ
ЁпЕуPЁЂMЁЂNЗжБ№ЮЊADЁЂABЁЂDEЕФжаЕуЃЌ
ЁрPM=![]() BDЃЌPMЁЮBDЃЌ
BDЃЌPMЁЮBDЃЌ
PN=![]() AEЃЌPNЁЮAEЃЌ
AEЃЌPNЁЮAEЃЌ
ЁрPM=PNЃЌ
ЁрЁЯMGE+ЁЯBHA=180ЁуЃЌ
ЁрЁЯMGE=90ЁуЃЌ
ЁрЁЯMPN=90ЁуЃЌ
ЁрPMЁЭPNЃЛ
ЃЈ3ЃЉгЩЃЈ2ЃЉПЩжЊЁїPMNЪЧЕШбќжБНЧШ§НЧаЮЃЌPM=![]() BDЃЌ
BDЃЌ
ЁрЕБBDЕФжЕзюДѓЪБЃЌPMЕФжЕзюДѓЃЌЁїPMNЕФУцЛ§зюДѓЃЌ
ЁрЕБBЁЂCЁЂDЙВЯпЪБЃЌBDЕФзюДѓжЕ=BC+CD=6ЃЌ
ЁрPM=PN=3ЃЌ
ЁрЁїPMNЕФУцЛ§ЕФзюДѓжЕ=![]() ЁС3ЁС3=
ЁС3ЁС3=![]() ЃЎ
ЃЎ