题目内容
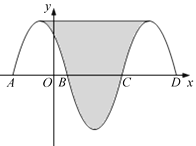
【题目】如图,抛物线y=﹣x2﹣2x+3与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1关于点B中心对称得C2,C2与x轴交于另一点C,将C2关于点C中心对称得C3,连接C1与C3的顶点,则图中阴影部分的面积为_________.
【答案】32
【解析】试题分析:∵抛物线y=﹣x2﹣2x+3与x轴交于点A、B,
∴当y=0时,则﹣x2﹣2x+3=0,
解得x=﹣3或x=1,
则A,B的坐标分别为(﹣3,0),(1,0),
AB的长度为4,
从C1,C3两个部分顶点分别向下作垂线交x轴于E、F两点.
根据中心对称的性质,x轴下方部分可以沿对称轴平均分成两部分补到C1与C2.
如图所示,阴影部分转化为矩形.
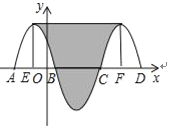
根据对称性,可得BE=CF=4÷2=2,则EF=8
利用配方法可得y=﹣x2﹣2x﹣3=﹣(x+1)2+4
则顶点坐标为(﹣1,4),即阴影部分的高为4,
S阴=8×4=32.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目