��Ŀ����
���ⱳ��:
��1�� ��ͼ1����ABC�У�DE��BC�ֱ�AB��AC��D��E���㣬����E��EF��AB��BC�ڵ�F���밴ͼʾ������գ�
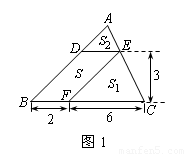
�ı���DBFE�����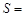 ��
��
��
��
��EFC�����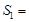 �� ��
�� ��
��ADE�����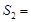 �� ��
�� ��
̽������
��1���ڣ�1���У���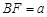 ��
��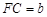 ��DE��BC��ľ���Ϊ
��DE��BC��ľ���Ϊ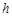 ����֤��
����֤��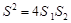 ��
��
��չǨ��
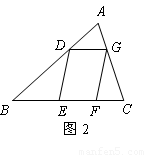
��2����ͼ2��ƽ���ı���DEFG���ĸ������ڡ�ABC�������ϣ�����ADG����DBE����GFC������ֱ�Ϊ2��5��3�������ã�2���еĽ������ABC�������
��1��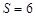 ��
��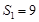 ��
��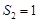 ��2����������3��18
��2����������3��18
���������⣺��1��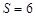 ��
��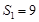 ��
��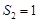 ��3�֣�
��3�֣�
��2��֤������DE��BC��EF��AB�����ı���DBFEΪƽ���ı��Σ�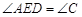 ��
�� ��
��
���ADE�ס�EFC����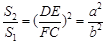 ��
��
��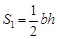 ����
����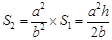 ��
��
��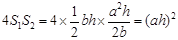 ����
����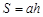 ����
����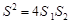 ��3�֣�
��3�֣�
��3���⣺����G��GH��AB��BC��H�����ı���DBHGΪƽ���ı��Σ�

��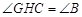 ��
��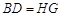 ��
��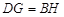 ��
��
���ı���DEFGΪƽ���ı��Σ�
��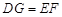 ��
��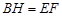 ��
��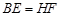 ��
��
���DBE�ա�GHF�����GHC�����Ϊ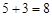 ��
��
�ɣ�2���ã���DBHG�����Ϊ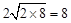 ��
��
���ABC�����Ϊ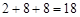 ��4�֣�
��4�֣�
��1���ı���DBFE��ƽ���ı��Σ����õס��߿����������EFC��������õס��ߵ�һ����㣻��ADG������������ȹ���A��AH��BC����DE��G����BC��H����AG�ǡ�ADE�ĸߣ�AH�ǡ�ABC�ĸߣ�����ƽ���߷��߶γɱ������������ۣ���֪��ADG�ס�ABC���������������ε�����ȵ������Ʊȵ�ƽ��������AG�������������ε������ʽ���㼴�ɣ�
��2������DE��BC��EF��AB����֪�ı���DBFE��▱��ͬʱ������ƽ���߷��߶γɱ������������ۣ���֪��ADE�ס�ABC����EFC�ס�ABC���Ӷ��á�ADE�ס�EFC���������������ε�����ȵ������Ʊȵ�ƽ�����ɵ�S1��S2=a2��b2������S1=1/2bh����ô����S2���Ӷ�����4S1S2����S=ah������֤�����ۣ�
��3������G��GH��AB��BC��H�����ı���DBHGΪƽ���ı��Σ�����֤����DBE�ա�GHF����ô��GHC���������8�������ã�2���еĽ��ۣ�����▱DBHG��������Ӷ������ABC�������

 �����Ƹ���ʦ����ϵ�д�
�����Ƹ���ʦ����ϵ�д� ��ͨ����ͬ����ϰ��ϵ�д�
��ͨ����ͬ����ϰ��ϵ�д� ����С����ͬ������ϵ�д�
����С����ͬ������ϵ�д�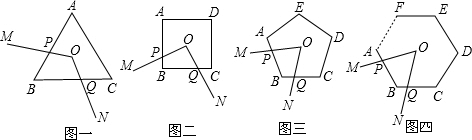
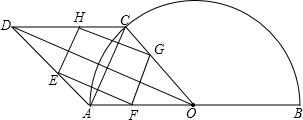 ֵ���жϴ�ʱ�ı���EFGH����״����˵�����ɣ�
ֵ���жϴ�ʱ�ı���EFGH����״����˵�����ɣ�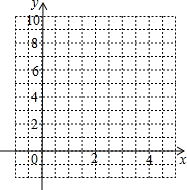 s����s��x�ĺ�����ϵʽΪ��
s����s��x�ĺ�����ϵʽΪ��