题目内容
16、问题背景:
A、B两家超市都有某种品牌的乒乓球拍和乒乓球出售,且每副球拍的标价都为50元,每个乒乓球的标价都为2元.现两家超市正在促销,A超市所有商品均打九折销售,而B超市买一副乒乓球拍送4个乒乓球.若仅考虑购买球拍和乒乓球的费用.
(1)如果只在某一家超市购一副乒乓球拍和10个乒乓球,问去A超市还是B超市买更合算?
迁移运用:
(2)某乒乓球训练馆准备购买n副该种品牌的乒乓球拍,每副球拍配k(k≥4)个乒乓球.如果只在某一家超市购买,问去A超市还是B超市买更合算?
拓展延伸:
(3)若乒乓球训练馆准备购买n副该种品牌的乒乓球拍,每副球拍配20个乒乓球.请通过计算设计出最省钱的购买方案.
A、B两家超市都有某种品牌的乒乓球拍和乒乓球出售,且每副球拍的标价都为50元,每个乒乓球的标价都为2元.现两家超市正在促销,A超市所有商品均打九折销售,而B超市买一副乒乓球拍送4个乒乓球.若仅考虑购买球拍和乒乓球的费用.
(1)如果只在某一家超市购一副乒乓球拍和10个乒乓球,问去A超市还是B超市买更合算?
迁移运用:
(2)某乒乓球训练馆准备购买n副该种品牌的乒乓球拍,每副球拍配k(k≥4)个乒乓球.如果只在某一家超市购买,问去A超市还是B超市买更合算?
拓展延伸:
(3)若乒乓球训练馆准备购买n副该种品牌的乒乓球拍,每副球拍配20个乒乓球.请通过计算设计出最省钱的购买方案.
分析:(1)A、B两家超市都有某种品牌的乒乓球拍和乒乓球出售,且每副球拍的标价都为50元,每个乒乓球的标价都为2元.现两家超市正在促销,A超市所有商品均打九折销售,而B超市买一副乒乓球拍送4个乒乓球可求出结果.
(2)单独在A超市购买费用为:(50n+2nk)×0.9元,单独在B超市购买费用为:50n+2n(k-4),讨论当去B超市更合算,去两家超市费用一样,去A超市更合算的情况.
(3)根据不同的方案求出结果看看那个最合算,方案一:单独在A超市购买费用为,方案二:单独在B超市购买费用为,方案三:设先在B超市买x副球拍后,再到A超市买余下的球拍和球.
(2)单独在A超市购买费用为:(50n+2nk)×0.9元,单独在B超市购买费用为:50n+2n(k-4),讨论当去B超市更合算,去两家超市费用一样,去A超市更合算的情况.
(3)根据不同的方案求出结果看看那个最合算,方案一:单独在A超市购买费用为,方案二:单独在B超市购买费用为,方案三:设先在B超市买x副球拍后,再到A超市买余下的球拍和球.
解答:解:(1)单独在A超市购买费用为:(50+10×2)×0.9=63(元);
单独在B超市购买费用为:50+(10-4)×2=62(元).
因此去B超市买更合算.(2分)
(2)单独在A超市购买费用为:(50n+2nk)×0.9元;
单独在B超市购买费用为:50n+2n(k-4)元.
当(50n+2nk)×0.9>50n+2n(k-4),即k<15时,去B超市买更合算;
当(50n+2nk)×0.9=50n+2n(k-4),即k=15时,去两家超市买费用一样;
当(50n+2nk)×0.9<50n+2n(k-4),即k>15时,去A超市买更合算;(8分)
(3)方案一:单独在A超市购买费用为:(50n+40n)×0.9=81n元;(9分)
方案二:单独在B超市购买费用为:50n+2n(20-4)=82n元.(10分)
方案三:设先在B超市买x副球拍后,再到A超市买余下的球拍和球,
设总费用为W.W=50x+[50(n-x)+2(20n-4x)]×0.9=-2.2x+81n.(13分)
因为n-x≥0且20n-4x≥0,
所以x≤n.(14分)
因为n为常数,W随x的增大而减小,
所以当x=n时,W=-2.2x+81n有最小值78.8n.
因为78.8n<81n<82n,
所以先在B超市买n副球拍后,再到A超市买余下16n个球,
总费用最小,最小费用为78.8n元.(15分)
单独在B超市购买费用为:50+(10-4)×2=62(元).
因此去B超市买更合算.(2分)
(2)单独在A超市购买费用为:(50n+2nk)×0.9元;
单独在B超市购买费用为:50n+2n(k-4)元.
当(50n+2nk)×0.9>50n+2n(k-4),即k<15时,去B超市买更合算;
当(50n+2nk)×0.9=50n+2n(k-4),即k=15时,去两家超市买费用一样;
当(50n+2nk)×0.9<50n+2n(k-4),即k>15时,去A超市买更合算;(8分)
(3)方案一:单独在A超市购买费用为:(50n+40n)×0.9=81n元;(9分)
方案二:单独在B超市购买费用为:50n+2n(20-4)=82n元.(10分)
方案三:设先在B超市买x副球拍后,再到A超市买余下的球拍和球,
设总费用为W.W=50x+[50(n-x)+2(20n-4x)]×0.9=-2.2x+81n.(13分)
因为n-x≥0且20n-4x≥0,
所以x≤n.(14分)
因为n为常数,W随x的增大而减小,
所以当x=n时,W=-2.2x+81n有最小值78.8n.
因为78.8n<81n<82n,
所以先在B超市买n副球拍后,再到A超市买余下16n个球,
总费用最小,最小费用为78.8n元.(15分)
点评:本题考查一次函数的应用,关键是根据不同的优惠方案表示出钱数,然后讨论B合算,A,B超市一样,B合算的情况,求出购买的数的不同,以及根据不同的方案,求出钱数,找到最省钱的方案.

练习册系列答案
相关题目
 (2013•宜昌)[背景资料]
(2013•宜昌)[背景资料]
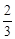 的人自带彩棉机采摘,
的人自带彩棉机采摘,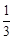 的人手工采摘,两家采摘完毕,采摘的天数刚好一样,张家付给雇工工钱总额为14400元,王家这次采摘棉花的总重量是多少?
的人手工采摘,两家采摘完毕,采摘的天数刚好一样,张家付给雇工工钱总额为14400元,王家这次采摘棉花的总重量是多少?