题目内容

问题背景：
在△ABC中，AB、BC、AC三边的长分别为
5
、
10
、
13
，求这个三角形的面积．
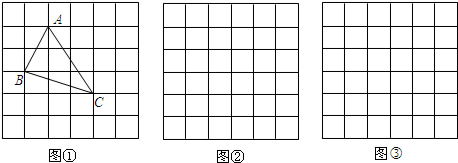
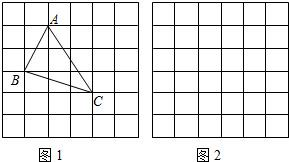
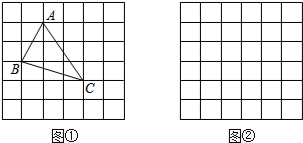
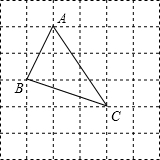
小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），如图①所示．这样不需求△ABC的高，而借用网格就能计算出它的面积．我们把上述求△ABC面积的方法叫做构图法．
（1）若△ABC三边的长分别为
5
a，2
2
a，
17
a（a＞0），请利用图②的正方形网格（每个小正方形的边长为a）画出相应的△ABC，并求出它的面积．
思维拓展：
（2）若△ABC三边的长分别为
m2+16n2
，
9m2+4n2
，2
m2+n2
（m＞0，n＞0，且m≠n），试运用构图法求出这三角形的面积．
探索创新：
（3）已知a、b都是正数，a+b=3，求当a、b为何值时
a2+4
+
b2+25
有最小值，并求这个最小值．
（4）已知a，b，c，d都是正数，且a2+b2=c2，c
a2-d2
=a2，求证：ab=cd．
分析：（1）
5
a是直角边长为a，2a的直角三角形的斜边；2
2
a是直角边长为2a，2a的直角三角形的斜边；
17
a是直角边长为a，4a的直角三角形的斜边，把它整理为一个矩形的面积减去三个直角三角形的面积；
（2）结合（1）易得此三角形的三边分别是直角边长为m，4n的直角三角形的斜边；直角边长为3m，2n的直角三角形的斜边；直角边长为2m，2n的直角三角形的斜边．同样把它整理为一个矩形的面积由（1）的结果可作BD=12，过点A作AF∥BD，交DE的延长线于F点，使AB=2，ED=3，连接AE交BD于点C，然后构造矩形AFDB，Rt△AFE，利用矩形的直角三角形的性质（3）可作BD=3，过点A作AF∥BD，交DE的延长线于F点，使AB=2，ED=5，连接AE交BD于点C，然后构造矩形AFDB，Rt△AFE，利用矩形的直角三角形的性质可求得AE的值就是代数式
a2+4
+
b2+25
的最小值．
（4）根据a2+b2=c2，c
a2-d2
=a2，得出c2（a2-d2）=a4，进而得出（a2+b2）（a2-d2）=a4，再去括号得出a2b2=d2c2，即可得出答案．
解答：解：（1）如图：

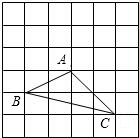
S△ABC=2a×4a-
1
2
a×2a-
1
2
×2a×2a-
1
2
a×4a=3a2；

（2）构造△ABC所示，（未在试卷上画出图形不扣分）

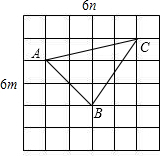
S△ABC=3m×4n-
1
2
×m×4n-
1
2
×3m×2n-
1
2
×2m×2n=5mn．  

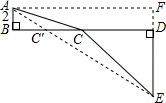
（3）如图所示：已知AB=2，DE=5，BD=3，
AB⊥BD，DE⊥BD，当AE在一条直线上时，AC+CE最小，
由题意得出：AB∥DE，
∴△ABC′∽△EDC′，
∴
AB
ED
=
BC′
C′D
，
∴
2
5
=
BC′
3-BC′
，
解得：BC′=
6
7
，C′D=3-
6
7
=
15
7
，
过点A作AF∥BD，交DE的延长线于F点，
根据题意，四边形ABDF为矩形．
EF=AB+DE=2+5=7，AF=DB=3．
∴AE=
49+9
=
58
．
即AC+CE的最小值是
58
，
故：a=
6
7
，b=3-
6
7
=
15
7
时，
a2+4
+
b2+25
有最小值为
58
．


（4）证明：∵a2+b2=c2，c
a2-d2
=a2，
∴c2（a2-d2）=a4，
则（a2+b2）（a2-d2）=a4，
整理得出：a2b2=a2d2+b2d2，
∴a2b2=d2（a2+b2），
∴a2b2=d2c2，
∵a，b，c，d都是正数，
∴ab=cd．
点评：此题主要考查了最短路线问题以及勾股定理应用，利用了数形结合的思想，通过构造直角三角形，利用勾股定理求解是解题关键．，关键是结合网格用矩形及容易求得面积的直角三角形表示出所求三角形的面积进行解答．
练习册系列答案
相关题目
问题背景：
在△ABC中，AB、BC、AC三边的长分别为
5
、
10
、
13
，求这个三角形的面积．
小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），如图①所示．这样不需求△ABC的高，而借用网格就能计算出它的面积．
（1）请你将△ABC的面积直接填写在横线上
 
；
思维拓展：
（2）我们把上述求△ABC面积的方法叫做构图法．若△ABC三边的长分别为
5
a、2
2
a、
17
a（a＞0），请利用图②的正方形网格（每个小正方形的边长为a）画出相应的△ABC，并求出它的面积；
探索创新：
（3）若△ABC三边的长分别为
m2+16n2
、
9m2+4n2
、2
m2+n2
（m＞0，n＞0，且m≠n），试运用构图法求出这三角形的面积．
精英家教网
问题背景：在△ABC中，AB、BC、AC三边的长分别为
5
、
10
、
13
，求这个三角形的面积小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶精英家教网点都在小正方形的顶点处），如图1所示．这样不需求△ABC的高，而借用网格就能计算出它的面积．
（1）请你将△ABC的面积直接填写在横线上．
 

（2）画△DEF，DE、EF、DF三边的长分别为
2
、
8
、
10

①判断三角形的形状，说明理由．
②求这个三角形的面积．
问题背景：在△ABC中，AB、BC、AC三边的长分别为
5
、
10
、
13
，求此三角形的面积．小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），如图①所示．这样不需求△ABC的高，而借用网格就能计算出它的面积．
（1）请你将△ABC的面积直接填写在横线上：
3.5
3.5
．
思维拓展：
（2）我们把上述求△ABC面积的方法叫做构图法．如果△ABC三边的长分别
5
a、
8
a、
17
a（a＞0），请利用图②的正方形网格（每个小正方形的边长为a）画出相应的△ABC，并求出它的面积．
问题背景：“在△ABC中，AB、BC、AC三边的长分别为
5
、
10
、
13
，求这个三角形的面积．”
小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网络中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），
（1）如图所示．这样不需求△ABC的高，而借用网格就能计算出它的面积是
3.5
3.5
．
（2）如图我们把上述求面积的方法叫做构图法．若△DCE三边的长分别为
m2+16n2
、
9m2+4n2
、
4m2+4n2
（m＞0，n＞0，且m≠n），试运用构图法求出这三角形的面积．
问题背景：在△ABC中，AB、BC、AC三边的长分别为
5
、
10
、
13
，求这个三角形BC边上的高．
杰杰同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处）．借用网格等知识就能计算出这个三角形BC边上的高．
（1）请在正方形网格中画出格点△ABC；
（2）求出这个三角形BC边上的高．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网