题目内容
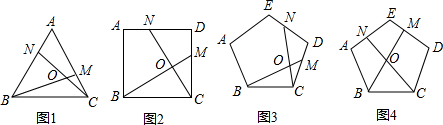
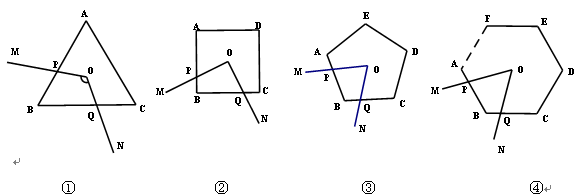
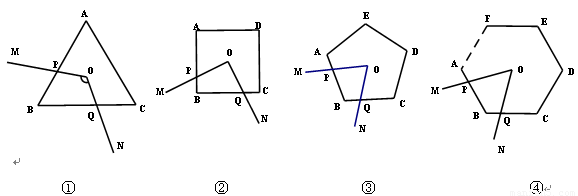
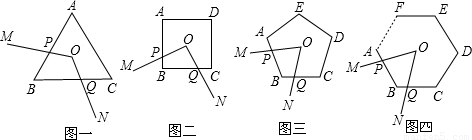
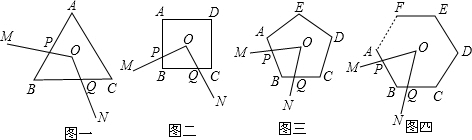
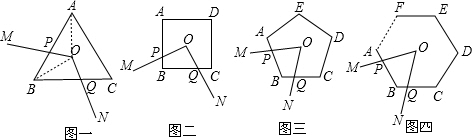
问题背景 某课外学习小组在一次学习研讨中,得到如下两个命题:①如图1,O是正三角形ABC的中心,∠MON分别与AB、BC交于点P,Q,若∠MON=120°,则四边形OPBQ的面积等于三角形ABC面积的三分之一.
②如图2,O是正方形ABCD的中心,∠MON分别与AB、BC交于点P,Q,若∠MON=90°,则四边形OPBQ的面积等于正方形ABCD面积的四分之一.
然后运用类比的思想提出了如下的命题:
③如图3,O是正五边形ABCDE的中心,∠MON分别与AB、BC交于点P,Q,若∠MON=72°,则四边形OPBQ的面积等于五边形ABCDE面积的五分之一.
任务要求
(1)请你从①、②、③三个命题中选择一个进行证明;
(2)请你继续完成下面的探索:
如图4,在正n(n≥3)边形ABCDEF…中,O是中心,∠MON分别与AB、BC交于点P,Q,若∠MON 等于多少度时,则四边形OPBQ的面积等于正n边形ABCDE…面积的n分之一?(不要求证明)
分析:(1)根据正三角形中心的性质得出,∠OAP=∠OBQ以及OA=OB,以及∠APO=∠BQO,进而得出△APO≌△BOQ,
再根据△OAB的面积与△ABC面积关系得出命题正确;
(2)根据规律得出一般公式即可得出∠MON的度数.
再根据△OAB的面积与△ABC面积关系得出命题正确;
(2)根据规律得出一般公式即可得出∠MON的度数.
解答:证明:(1)连接OA,OB,
∵OA=OB,∠OAP=∠OBQ,∠ABC+∠POQ=180°,
所以∠OPB+∠OQB=180°,∠APO=∠BQO,
∴△APO≌△BOQ,
所以四边形OPBQ的面积=三角形OAB的面积.
∴四边形OPBQ的面积等于三角形ABC面积的三分之一.
所以结论①成立.
(2)∠MON=(180°-
)=
度.
∵OA=OB,∠OAP=∠OBQ,∠ABC+∠POQ=180°,
所以∠OPB+∠OQB=180°,∠APO=∠BQO,
∴△APO≌△BOQ,
所以四边形OPBQ的面积=三角形OAB的面积.
∴四边形OPBQ的面积等于三角形ABC面积的三分之一.
所以结论①成立.

(2)∠MON=(180°-
| (n-2)•180 |
| n |
| 360 |
| n |
点评:此题主要考查了正三角形中心的性质以及全等三角形的证明,熟练应用正三角形中心的性质得出,∠OAP=∠OBQ以及△OAB的面积与△ABC面积关系是解决问题的关键.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目