题目内容
【题目】已知AB∥CD,点E为AB,CD之外任意一点.
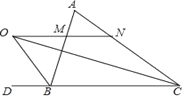
(1)如图1,探究∠BED与∠B,∠D的数量关系,并说明理由;
(2)如图2,探究∠CDE与∠B,∠E的数量关系,并说明理由.
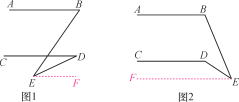
【答案】(1) ∠B=∠BED+∠D. (2)∠CDE=∠B+∠BED.
【解析】
在①中过点E作EF∥AB,由平行线的性质可得∠BEF=∠B,∠D=∠DEF,再根据∠BEF=∠BED+∠DEF等量代换即可得到结果;在②中过点E作EF∥AB,同①的方法,可找到∠BED与∠B、∠CDE的数量关系.
解:(1)∠B=∠BED+∠D.理由如下:
过点E作EF∥AB.
又∵AB∥CD,
∴EF∥AB∥CD.
∴∠BEF=∠B,∠D=∠DEF.
∵∠BEF=∠BED+∠DEF,
∴∠B=∠BED+∠D.
(2)∠CDE=∠B+∠BED.理由如下:
过点E作EF∥AB.
又∵AB∥CD,
∴EF∥AB∥CD.
∴∠B+∠BEF=180°,∠CDE+∠DEF=180°.
又∵∠DEF=∠BEF-∠BED,
∴∠CDE+∠BEF-∠BED=∠B+∠BEF,
即∠CDE=∠B+∠BED.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目