题目内容
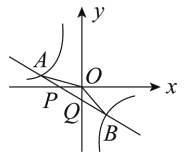
【题目】在平面直角坐标系xOy中,抛物线M:y=-x2+2bx+c与直线l:y=9x+14交于点A,其中点A的横坐标为-2.
(1)请用含有b的代数式表示c: ;
(2)若点B在直线l上,且B的横坐标为-1,点C的坐标为(b,5).
①若抛物线M还过点B,直接写出该抛物线的解析式;
②若抛物线M与线段BC恰有一个交点,结合函数图象,直接写出b的取值范围.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() 或
或![]() .
.
【解析】
(1)将A点横坐标,代入直线l:y=9x+14得到A点的坐标,再代入到抛物线中,即可求解;
(2)①将B点横坐标,代入直线l:y=9x+14得到B点的坐标,再代入到抛物线中,可求出抛物线的解析式;
②抛物线的顶点为N(![]() ),开口向下,C(b,5),B(-1,5),要使得抛物线M与线段BC有交点,N不在C的下方,即
),开口向下,C(b,5),B(-1,5),要使得抛物线M与线段BC有交点,N不在C的下方,即![]()
![]() 0,则分
0,则分![]() ,或
,或![]() 两种情况讨论,结合图象求解.
两种情况讨论,结合图象求解.
解:(1)∵抛物线M:y=-x2+2bx+c与直线l:y=9x+14交于点A,其中点A的横坐标为-2,
∴A(-2,-4),
代入y=-x2+2bx+c得![]() ,
,
∴![]() .
.
故答案为:![]() .
.
(2)∵点B在直线l:y=9x+14上,且B的横坐标为-1,
∴B(-1,5),
①若抛物线M:y=-x2+2bx+4b还过点B(-1,5),
∴![]() ,
,
∴b=3,
∴该抛物线的解析式:![]() ;
;
②∵![]() 的顶点为N(
的顶点为N(![]() ),开口向下,
),开口向下,
其中C(b,5),B(-1,5),
要使得抛物线M与线段BC有交点,N不在C的下方,即![]() 0,
0,
∴![]() ,或
,或![]() ,
,
当![]() 时,
时,

结合函数图象,若抛物线M与线段BC恰有一个交点,
当![]() 时,
时,![]() ,
,
∴![]() ;
;
当![]() 时,
时,
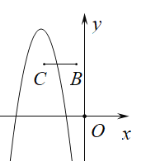
结合函数图象,若抛物线M与线段BC恰有一个交点,
当![]() 时,
时,![]() ,
,
∴![]() ;
;
综上所述:抛物线M与线段BC恰有一个交点时,![]() 或
或![]() .
.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案【题目】某公司为了到高校招聘大学生,为此设置了三项测试:笔试、面试、实习.学生的最终成绩由笔试面试、实习依次按3:2:5的比例确定.公司初选了若干名大学生参加笔试,面试,并对他们的两项成绩分别进行了整理和分析.下面给出了部分信息:
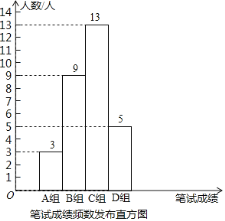
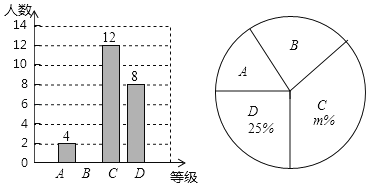
①公司将笔试成绩(百分制)分成了四组,分别为A组:60≤x<70,B组:70≤x<80,C组:80≤x<90,D组:90≤x<100;并绘制了如下的笔试成绩频数分布直方图.其中,C组的分数由低到高依次为:80,81,82,83,83,84,84,85,86,88,88,88,89.
②这些大学生的笔试、面试成绩的平均数、中位数、众数、最高分如下表:
平均数 | 中位数 | 众数 | 最高分 | |
笔试成绩 | 81 | m | 92 | 97 |
面试成绩 | 80.5 | 84 | 86 | 92 |
根据以上信息,回答下列问题:
(1)这批大学生中笔试成绩不低于88分的人数所占百分比为 .
(2)m= 分,若甲同学参加了本次招聘,他的笔试、面试成绩都是83分,那么该同学成绩排名靠前的是 成绩,理由是 .
(3)乙同学也参加了本次招聘,笔试成绩虽不是最高分,但也不错,分数在D组;面试成绩为88分,实习成绩为80分由表格中的统计数据可知乙同学的笔试成绩为 分;若该公司最终录用的最低分数线为86分,请通过计算说明,该同学最终能否被录用?