题目内容
【题目】如图,已知AC、BD相交于点O,AD=BC,AE⊥BD于点E,CF⊥BD于点F,BE=DF.求证:
(1)△ADE≌△CBF;
(2)OA=OC.
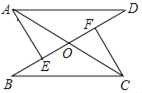
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)由BE=DF,可得BF=DE,则根据“HL”可证Rt△ADE≌Rt△CBF;
(2)由Rt△ADE≌Rt△CBF可得AE=CF,根据“AAS”可证△AOE≌△COF,可得OA=OC.
证明:(1)∵BE=DF
∴BE+EF=DF+EF
∴BF=DE,且AD=BC
∴Rt△ADE≌Rt△CBF(HL)
(2)∵Rt△ADE≌Rt△CBF
∴AE=CF,且∠AEO=∠CFO=90°,∠AOE=∠COF
∴△AOE≌△COF(AAS)
∴OA=OC

练习册系列答案
相关题目