题目内容
【题目】在△ABC中,CD是△ABC的中线,如果![]() 上的所有点都在△ABC的内部或边上,则称
上的所有点都在△ABC的内部或边上,则称![]() 为△ABC的中线弧.
为△ABC的中线弧.
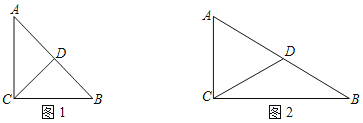
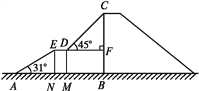
(1)在Rt△ABC中,∠ACB=90°,AC=1,D是AB的中点.
①如图1,若∠A=45°,画出△ABC的一条中线弧![]() ,直接写出△ABC的中线弧
,直接写出△ABC的中线弧![]() 所在圆的半径r的最小值;
所在圆的半径r的最小值;
②如图2,若∠A=60°,求出△ABC的最长的中线弧![]() 的弧长l.
的弧长l.
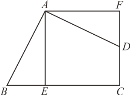
(2)在平面直角坐标系中,已知点A(2,2),B(4,0),C(0,0),在△ABC中,D是AB的中点.求△ABC的中线弧![]() 所在圆的圆心P的纵坐标t的取值范围.
所在圆的圆心P的纵坐标t的取值范围.
【答案】(1)①图见解析,![]() ,②
,②![]() ;(2)t≥5或t≤﹣
;(2)t≥5或t≤﹣![]()
【解析】
(1)①如图1中,当中线弧![]() 的圆心是AC或BC的中点时,
的圆心是AC或BC的中点时,![]() 所在圆的半径r的最小.
所在圆的半径r的最小.
②如图2中,当中线弧![]() 所在的圆与AC,AB都相切时,
所在的圆与AC,AB都相切时,![]() 的弧长最大.
的弧长最大.
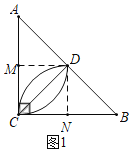
(2)分两种情形:如图3中,若中线弧在 线段CD的下方时,如图4中,若中线弧![]() 在 线段CD的上方时,分别求解即可解决问题.
在 线段CD的上方时,分别求解即可解决问题.
解:(1)①如图1中,当直线弧![]() 的圆心是AC或BC的中点时,
的圆心是AC或BC的中点时,![]() 所在圆的半径r的最小,
所在圆的半径r的最小,
当∠A=45°,
此时r=![]() AC=
AC=![]() ,
,
∴△ABC的中线弧![]() 所在圆的半径r的最小值为
所在圆的半径r的最小值为![]() .
.
②如图2中,当中线弧![]() 所在的圆与AC,AB都相切时,
所在的圆与AC,AB都相切时,![]() 的弧长最大,
的弧长最大,
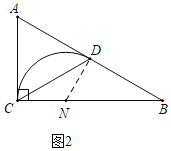
此时,![]() 的圆心在BC上,
的圆心在BC上,
∵ND⊥BD,
∴∠NDB=90°,
∵∠A=60°,∠ACB=90°,
∴∠B=30°,
∴BN=2DN=2CN,
∴3CN=BC=![]() ,
,
∴CN=![]() ,
,
∴半径为![]() .
.
∴△ABC的最长的中线弧![]() 的弧长l
的弧长l![]() ;
;
(2)如图3中,若中线弧![]() 在 线段CD的下方时,
在 线段CD的下方时,
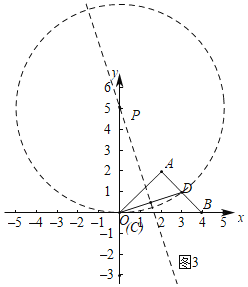
∵△ABC的中线弧![]() 所在的圆的圆心在线段CD使得垂直平分线上,
所在的圆的圆心在线段CD使得垂直平分线上,
当中线弧![]() 所在圆与BC相切时,可得P(0,5),
所在圆与BC相切时,可得P(0,5),
观察图象可知中线弧![]() 所在圆的圆心P的纵坐标t≥5.
所在圆的圆心P的纵坐标t≥5.
如图4中,若中线弧![]() 在 线段CD的上方时,
在 线段CD的上方时,
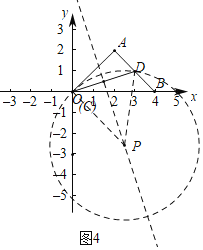
当中线弧![]() 所在圆与AC相切时,可得P(
所在圆与AC相切时,可得P(![]() ,﹣
,﹣![]() ),
),
观察图象可知中线弧![]() 所在圆的圆心P的纵坐标t≤﹣
所在圆的圆心P的纵坐标t≤﹣![]() .
.
综上所述,中线弧![]() 所在圆的圆心P的纵坐标t的取值范围为:t≥5或t≤﹣
所在圆的圆心P的纵坐标t的取值范围为:t≥5或t≤﹣![]() .
.

 口算题卡加应用题集训系列答案
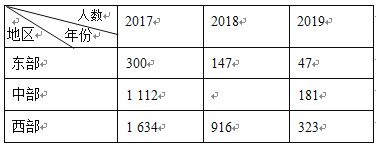
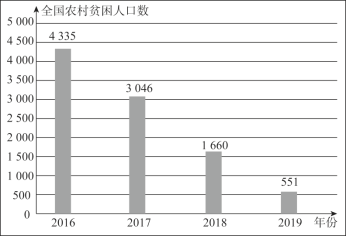
口算题卡加应用题集训系列答案【题目】人口数据又称为人口统计数据,是指国家和地区的相关人口管理部门通过户口登记、人口普査等方式统计得出的相关数据汇总.人口数据对国家和地区的人口状况、管理以及各项方针政策的制定都具有重要的意义.下面是关于人口数据的部分信息.
a.2018年中国大陆(不含港澳台)31个地区人口数量(单位:千万人)的频数分布直方图(数据分成6组:0≤x<2,2≤x<4,4≤x<6,6≤x<8,8≤x<10,10≤x≤12):
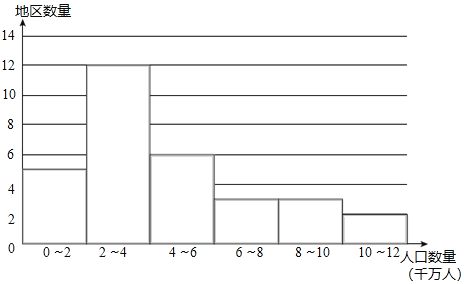
b.人口数量在2≤x<4这一组的是:
2.2 2.4 2.5 2.5 2.6 2.7 3.1 3.6 3.7 3.8 3.9 3.9
c.2018年中国大陆(不含港澳台)31个地区人口数量(单位:千万人)、出生率(单位:‰)、死亡率(单位:‰)的散点图:
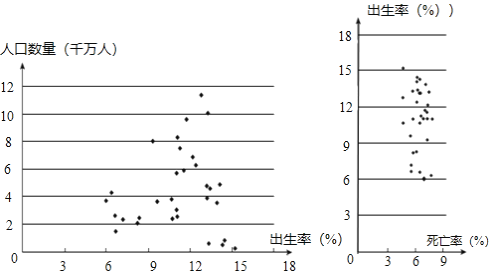
d.如表是我国三次人口普查中年龄结构构成情况:
0~14岁人口比例 | 15~59岁人口比例 | 60岁以上人口比例 | |
第二次人口普查 | 40.4% | 54.1% | 5.5% |
第五次人口普查 | 22.89% | 66.78% | 10.33% |
第六次人口普查 | 16.6% | 70.14% | 13.26% |
e.世界各国的人口出生率差别很大,出生率可分为五等,最高>50‰,最低<20‰,2018年我国人口出生率降低至10.94‰,比2017年下降1.43个千分点.
根据以上信息,回答下列问题:
(1)2018年北京人口为2.2千万人,我国大陆(不含港澳台)地区中,人口数量从低到高排列,北京排在第 位.
(2)人口增长率=人口出生率﹣人口死亡率,我国大陆(不含港澳台)地区中人口在2018年出现负增长的地区有 个,在这些地区中,人口数量最少的地区人数为 千万人(保留小数点后一位).
(3)下列说法中合理的是 .
①我国人口基数较大,即使是人口出生率和增长率都缓慢增长的前提下,人口总数仍然是在不断攀升的,所以我国计划生育的基本国策是不变的;
②随着我国老龄化越来越严重,所以出台了“二孩政策”,目的是为了缓解老龄化的压力.