Question

如图，在直角坐标系中，正方形ABOD的边长为a，O为原点，点B在x轴的负半轴上，点D在y轴的正半轴上，直线OE的解析式为y=2x，直线CF过x轴上的一点C（-

3

5

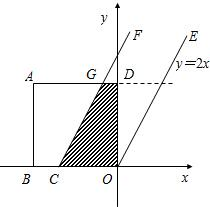a，0）且与OE平行，现正方形以每秒

a

10

的速度匀速沿x轴正方向平行移动，设运动时间为t秒，正方形被夹在直线OE和CF间的部分的面积为S．
（1）当0≤t＜4时，写出S与t的函数关系式；
（2）当4≤t≤5时，写出S与t的函数关系式，在这个范围内S有无最大值？若有，请求出最大值，若没有请说明理由．

Answer 1

分析：（1）易知BC=

2

5

a，根据时间的取值范围和正方形的速度可知当0≤t＜4时，B位于C点左侧．那么重合部分的多边形的面积可用平行四边形的面积-△NPQ的面积来求解．可先求出P、C的坐标，然后根据△PNQ与△PDO相似，用相似比求出面积比，进而得出△PNQ的面积．然后按上面所说的多边形的面积计算方法得出S，t的函数关系式；
（2）当4≤t≤5时，重合部分可用平行四边形COPG的面积-△PNQ的面积-△CB1R的面积来求得．方法同（1），得出S，t的函数关系后，可根据函数的性质和自变量的取值范围求出S的最大值及对应的t的值．

解答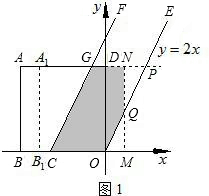：解：（1）当0≤t＜4时，如图1，由图可知OM=

a

10

t，
设经过t秒后，正方形移动到A₁B₁MN
∵当t=4时，BB₁=OM=

a

10

×4=

2

5

a
∴点B₁在C点左侧
∴夹在两平行线间的部分是多边形COQNG，其面积为：
平行四边形COPG-△NPQ的面积．
∵CO=

3

5

a，OD=a
∴四边形COPG面积=

3

5

a²
又∵点P的纵坐标为a，代入y=2x得P（

a

2

，a）
∴DP=

a

2

，NP=

a

2

-

a

10

t
由y=2x知：NQ=2NP
∴△NPQ面积=

1

2

•NP•NQ=（

a

2

-

a

10

t）²
∴S=

3

5

a²-（

a

2

-

a

10

t）²=

3

5

a²-

a2

100

（5-t）²=

a2

100

[60-（5-t）²]；

（2）当4≤t≤5时，如图2，这时正方形移动到A₁B₁MN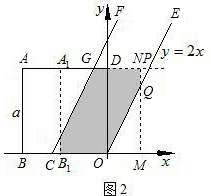
∵当4≤t≤5时，

2

5

a≤BB₁≤

1

2

a，点B₁在C、O点之间
∴夹在两平行线间的部分是B₁OQNGR，
即平行四边形COPG被切掉了两个小三角形△NPQ和△CB₁R，其面积为：
平行四边形COPG的面积-△NPQ的面积-△CB₁R的面积
与（1）同理，OM=

a

10

t，NP=

a

2

-

a

10

t，S_△NPQ=（

a

2

-

a

10

t）²，
∵CO=

3

5

a，CM=

3

5

a+

a

10

t，B₁M=a，
∴CB₁=CM-B₁M=

3

5

a+

a

10

t-a=

a

10

t-

2

5

a，
∴S△CB₁R=

1

2

CB₁•B₁R=（CB₁）²=（

a

10

t-

2

5

a）2，
∴S=

3

5

a²-（

1

2

a-

a

10

t）²-（

a

10

t-

2

5

a）²=

3

5

a²-

a2

100

[2（t-

9

2

）²+

1

2

]，
∴当t=

9

2

时，S有最大值，Smax=

119

200

a²．

点评：本题考查二次函数与相似三角形、平行四边形、正方形、图形的面积求法等知识的综合运用．