题目内容
【题目】甲、乙两个工程队同时开始维修某一段路面,一段时间后,甲队被调往别处,乙队又用了2小时完成了剩余的维修任务.已知乙队每小时维修路面的长度保持不变,甲队每小时维修路面30米.甲、乙两队在此路段维修路面的总长度y(米)与维修时间x(时)之间的函数图象如图所示. 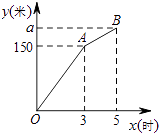
(1)甲队调离时,甲、乙两队已维修路面的总长度为
(2)求此次维修路面的总长度a.
(3)求甲队调离后y与x之间的函数关系式.
【答案】
(1)150
(2)解:甲队调离前,甲、乙两队每小时维修路面的总长度为150÷3=50(米).
∴乙队每小时维修路面的长度为50﹣30=20,
a=150+20×2=190(米)
(3)解:设所求函数关系式为y=kx+b.
将点(3,150),(5,190)代入,得
![]() ,解得
,解得 ![]() .
.
故甲队调离后y与x之间的函数关系式为:y=20x+90(3<x≤5).
【解析】解:(1)甲队调离时,甲、乙两队已维修路面的总长度为150米,
所以答案是:150.

练习册系列答案
相关题目