题目内容

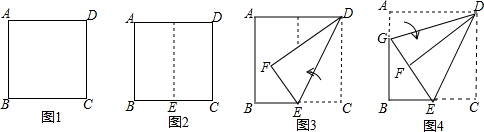
如图，将边长为8cm的正方形ABCD折叠，使点D落在BC边的中点E处，点A落在F处，折痕为MN，求线段CN长．
设CN=xcm，则DN=（8-x）cm，由折叠的性质知EN=DN=（8-x）cm，
而EC=
1
2
BC=4cm，在Rt△ECN中，由勾股定理可知EN2=EC2+CN2，
即（8-x）2=16+x2，
整理得16x=48，
解得：x=3．
即线段CN长为3．
练习册系列答案
相关题目
如图，有一矩形纸片ABCD，AB=6，AD=8，将纸片折叠，使AB落在AD边上，折痕为AE，再将△AEB以BE为折痕向右折叠，AE与DC交于点F，则
FC
CD
的值是（　　）
A．1B．
1
2
C．
1
3
D．
1
4
如图，扇形OAB的圆心角为直角，正方形OCDE的顶点分别在OA、OB、弧AB上，AF⊥ED，交ED的延长线于点F，如果正方形OCDE的边长为1，图中阴影部分面积为______．
如图，矩形纸片ABCD中，AB=18cm，把矩形纸片沿直线AC折叠，点B落在点E处，AE交DC于点F，若AF=13，则AD的长为（　　）
A．5cmB．6cmC．10cmD．12cm
由16个相同的小正方形拼成的正方形网格，现将其中的三小正方形涂黑（如图）．请你用两种不同的方法分别在图中再将两个空白的小正方形涂上阴影，使它们成为轴对称图形．
如图，已知AB⊥AD，CD⊥AD，垂足分别为A、D，AD=6，AB=5，CD=3，P是线段AD上的一个动点，设AP=x，DP=y，a=
x2+25
+
y2+9
，则a的最小值是______．
函数f(x)=
x2+1
+
(4-x)2+4
的最小值是______．
【多彩数学】
如何将正方形的边三等分和五等分
给你一张如图1的正方形纸片，让你用折纸的方法将其中一边二、四等分，你会轻而易举地用对折的方法完成．可是让你将正方形的一边三等分或五等分呢？我们先来三等分边长．

（1）对折，使E为BC中点（图2）；
（2）连结DE，沿DE将DC翻折到DF位置（图3）；
（3）使点A与点F重合（图4），那么AG=
1
3
AB，G为AB的三等分点．
下面请你试一试将正方形一边长五等分的折叠方法写出来．
（1）如图，在“4×4”正方形网格中，已有2个小正方形被涂黑．请你分别在下面2张图中再将若干个空白的小正方形涂黑，使得涂黑的图形成为轴对称图形．（图（1）要求只有1条对称轴，图（2）要求只有2条对称轴）．
（2）如图，A、B为直线MN外两点，且到MN的距离不相等．分别在MN上求一点P，并满足如下条件：
①在图（3）中求一点P使得PA+PB最小；②在图（4）中求一点P使得|PA-PB|最大．
（不写作法，保留作图痕迹）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网