题目内容
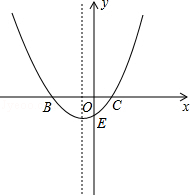
(2013年四川攀枝花12分)如图,抛物线y=ax2+bx+c经过点A(﹣3,0),B(1.0),C(0,﹣3).
(1)求抛物线的解析式;
(2)若点P为第三象限内抛物线上的一点,设△PAC的面积为S,求S的最大值并求出此时点P的坐标;
(3)设抛物线的顶点为D,DE⊥x轴于点E,在y轴上是否存在点M,使得△ADM是直角三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
解:(1)由于抛物线y=ax2+bx+c经过A(﹣3,0),B(1,0),可设抛物线的解析式为:y=a(x+3)(x﹣1),
将C点坐标(0,﹣3)代入,得:a(0+3)(0﹣1)=5,解得 a=1。
∴抛物线的解析式为:y=(x+3)(x﹣1),即y=x2+2x﹣3。
(2)如图1,过点P作x轴的垂线,交AC于点N.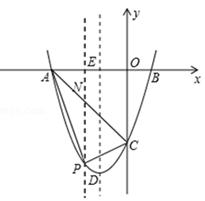
设直线AC的解析式为y=kx+m,由题意,得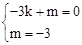 ,解得
,解得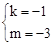 。
。
∴直线AC的解析式为:y=﹣x﹣3。
设P点坐标为(x,x2+2x﹣3),
则点N的坐标为(x,﹣x﹣3),
∴PN=PE﹣NE=﹣(x2+2x﹣3)+(﹣x﹣3)=﹣x2﹣3x。
∵S△PAC=S△PAN+S△PCN,
∴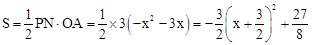 。
。
∴当x=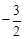 时,S有最大值
时,S有最大值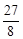 ,此时点P的坐标为(
,此时点P的坐标为(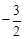 ,
,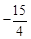 )。
)。
(3)在y轴上是否存在点M,能够使得△ADE是直角三角形。理由如下:
∵y=x2+2x﹣3=y=(x+1)2﹣4,∴顶点D的坐标为(﹣1,﹣4)。
∵A(﹣3,0),∴AD2=(﹣1+3)2+(﹣4﹣0)2=20。
设点M的坐标为(0,t),分三种情况进行讨论:
①当A为直角顶点时,如图2,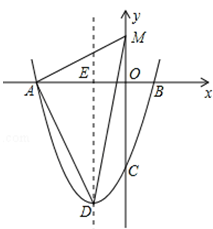
由勾股定理,得AM2+AD2=DM2,
即(0+3)2+(t﹣0)2+20=(0+1)2+(t+4)2,解得t=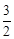 。
。
∴点M的坐标为(0,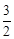 )。
)。
②当D为直角顶点时,如图3,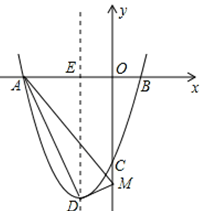
由勾股定理,得DM2+AD2=AM2,
即(0+1)2+(t+4)2+20=(0+3)2+(t﹣0)2,解得t=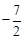 。
。
∴点M的坐标为(0,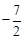 )。
)。
③当M为直角顶点时,如图4,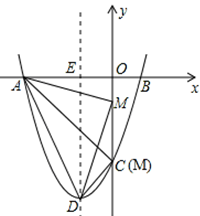
由勾股定理,得AM2+DM2=AD2,
即(0+3)2+(t﹣0)2+(0+1)2+(t+4)2=20,解得t=﹣1或﹣3。
∴点M的坐标为(0,﹣1)或(0,﹣3)。
综上所述,在y轴上存在点M,能够使得△ADE是直角三角形,此时点M的坐标为(0,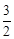 )或(0,
)或(0,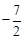 )或(0,﹣1)或(0,﹣3)。
)或(0,﹣1)或(0,﹣3)。
解析

 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 与y轴交于点C(0,-4),与x轴交于点A,B,且B点的坐标为(2,0)
与y轴交于点C(0,-4),与x轴交于点A,B,且B点的坐标为(2,0)

 )在直线MG上。问:当m为何值时,在抛物线C3上存在点Q,使得以M、N、P、Q为顶点的四边形为平行四边形?
)在直线MG上。问:当m为何值时,在抛物线C3上存在点Q,使得以M、N、P、Q为顶点的四边形为平行四边形?


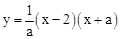 (a>0)与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.
(a>0)与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.