题目内容
【题目】如图,在△ABC中,
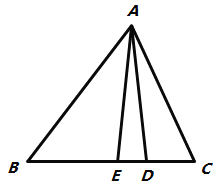
(1)若AE平分∠BAC,AD⊥BC于点D,∠C=74°,∠B=46°,求∠DAE的度数.
(2)若AE是△ABC的中线,BC=4,△ABE的面积为4,EC=3DE,求△ABC面积和△ADE的面积.
【答案】(1)14°;(2)8,![]()
【解析】
(1)根据角平分线和高的性质,结合三角形内角和定理求解;(2)根据三角形的中线性质,结合三角形的面积公式求解.
解:(1)∵∠B=46°,∠C=74°
∴∠BAC=180°-∠B-∠C=60°
∵AE平分∠BAC,
∴∠BAE=![]() ∠BAC=30°,
∠BAC=30°,
∵∠AD⊥BC,
∴∠ADB=90°,
∴∠BAD=90°-∠B=44°
∴∠DAE=∠BAD-∠BAE=44°-30°=14°;
(2)∵AE是△ABC的中线,
∴BE=EC,
∵S△ABE=![]() , S△AEC=
, S△AEC=![]() ,
,
∴S△ABE=S△AEC=4,
∴S△ABC=8,
∵EC=3DE,
∴DE=![]() EC,
EC,
∴S△ADE=![]() S△AEC=
S△AEC=![]() .
.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目



