题目内容
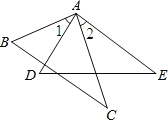
【题目】在△ABC中，AD平分∠BAC交BC于点D，在AB上取一点E，使得EA=ED.
（1）求证：DE∥AC；
（2）若ED=EB，BD=2，EA=3，求AD的长.
【答案】（1）见解析（2）4
【解析】
（1）根据等腰三角形的性质即可求解；
（2）根据已知条件得到∠ADB=90°，再利用Rt△ABD中，由勾股定理即可求解.
（1）证明：∵AD平分∠BAC，
∴∠1=∠2.
∵EA=ED,
∴∠1=∠3.
∴∠2=∠3.
∴DE∥AC.
（2）∵ED=EB，ED=EA,
∴∠B=∠4，ED=EB=EA=3.
∴AB=6.
在△ABD中，∠B+∠4+∠3+∠1=180°，
∵∠1=∠3，∠B=∠4，
∴∠B+∠4+∠3+∠1=2∠3+2∠4=180°.
∴∠ADB=∠3+∠4=90°.
在Rt△ABD中，由勾股定理得：
练习册系列答案
相关题目
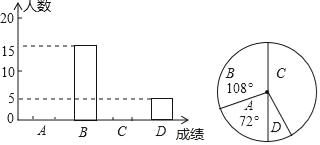
【题目】某校九年级数学测试后，为了解学生学习情况，随机抽取了九年级部分学生的数学成绩进行统计，得到相关的统计图表如下．
成绩/分 | 120﹣111 | 110﹣101 | 100﹣91 | 90以下 |
成绩等级 | A | B | C | D |
请根据以上信息解答下列问题：
（1）这次统计共抽取了 名学生的数学成绩，补全频数分布直方图；
（2）若该校九年级有1000名学生，请据此估计该校九年级此次数学成绩在B等级以上（含B等级）的学生有多少人？
（3）根据学习中存在的问题，通过一段时间的针对性复习与训练，若A等级学生数可提高40%，B等级学生数可提高10%，请估计经过训练后九年级数学成绩在B等级以上（含B等级）的学生可达多少人？
