题目内容
【题目】
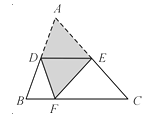
如图,在![]() 中,已知
中,已知![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 上的动点(不与端点重合),点
上的动点(不与端点重合),点![]() 是线段
是线段![]() 上的动点,连接
上的动点,连接![]() 、
、![]() ,若在点
,若在点![]() 、点
、点![]() 的运动过程中,始终保证
的运动过程中,始终保证![]() 。
。
(1)求证:![]() ;
;
(2)当以点![]() 为圆心,以
为圆心,以![]() 为半径的圆与
为半径的圆与![]() 相切时,求
相切时,求![]() 的长;
的长;
(3)探究:在点![]() 、点
、点![]() 的运动过程中,
的运动过程中,![]() 可能为等腰三角形吗?若能,求出
可能为等腰三角形吗?若能,求出![]() 的长;若不能,请说明理由。
的长;若不能,请说明理由。
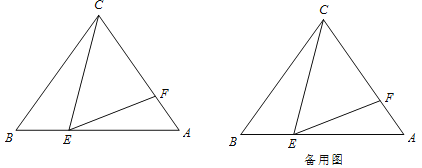
【答案】(1)证明见解析;(2)BE的长为1或5;(3)当BE的长为1或![]() 时,△CFE为等腰三角形.
时,△CFE为等腰三角形.
【解析】试题分析(1)由∠B +∠B CE=∠CEA=∠CEF+∠FEA,∠CEF=∠B即可得∠AEF=∠BCE;(2)设⊙C与BA切于点M,则CM=CF,CM⊥BA(如图),根据等腰三角形的性质可得BM=AM==3,在Rt△AMC中,根据勾股定理可得CF =CM=4,即可得AF=1,再证得△AEF∽△BCE,设设BE长为x,则EA长为6-x,根据相似三角形的性质列出方程求解即可;(3)分CE=CF,CF=EF,CF=EF三种情况求解即可.
试题解析:
(1)证明:∵∠B +∠B CE=∠CEA =∠CEF+∠FEA
∠CEF=∠B
∴∠AEF=∠BCE
(2)设⊙C与BA切于点M,则CM=CF,CM⊥BA
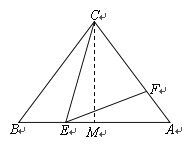
∵CA=CB,CM⊥BA ∴BM=AM=![]() =3
=3
Rt△AMC中,AC=5,AM=3,
∴CF =CM=4 ∴AF=1
∵ CA=CB ∴∠B=∠C
由(1)知∠AEF=∠BCE
∴△AEF∽△BCE
∴![]()
设BE长为x,则EA长为6-x
∴![]()
解得:x1=1,x2=5
答:BE的长为1或5.
(3)可能.

①当CE=CF时,∠3=∠2=∠A
∴EF∥AB,此时E与B重合,与条件矛盾,不成立.
②当CF=EF时,
又∵△AEF∽△BCE
∴△AEF≌△BCE
∴AE=BC=5
∴BE=AB-5=1
③当CF=EF时,∠1=∠2=∠A=∠B
△FCE∽△CBA
∴![]()

∴![]()
∵△AEF∽△BCE
∴![]()
∴![]()
∴![]()
答:当BE的长为1或![]() 时,△CFE为等腰三角形.
时,△CFE为等腰三角形.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案