Question

【题目】如图，已知四边形ABDE是平行四边形，C为边BD延长线上一点，连结AC、CE，使AB=AC．
（1）求证：△BAD≌△ACE；
（2）若∠B=30°，AB=26，BD=10，求平行四边形ABDE的面积．

Answer 1

【答案】
（1）证明：∵AB=AC，

∴∠B=∠ACB．

又∵四边形ABDE是平行四边形

∴AE∥BD，AE=BD，

∴∠ACB=∠CAE=∠B，

在△DBA和△EAC中

，

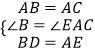∴△BAD≌△ACE（SAS）；

（2）解：过D作DM⊥AB于点M，

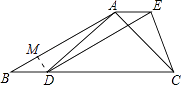
∵DB=10，

∴DM= DB=5，

∴平行四边形ABDE的面积=26×5=130．

【解析】（1）根据平行四边形的性质得出，再利用全等三角形的判定方法得出即可；（2）过D作DM⊥AB于点M，根据30°角的性质可求DM的长，再利用平行四边形的面积公式计算即可．
【考点精析】通过灵活运用平行四边形的性质，掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分即可以解答此题．