��Ŀ����
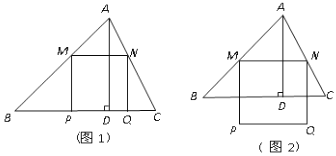
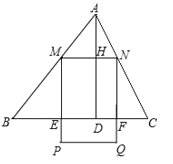
����Ŀ�������ABC�У�BC=6��S��ABC=12��������M��N�ֱ��ڱ�AB��AC�ϻ�������MN��BC����MNΪ��������������MPQN������߳�Ϊx��������MPQN����ABC�������ֵ����Ϊy(y>0)��
(1)��ABC�б�BC�ϸ�AD=______.
(2)��x=______ʱ��PQǡ�����ڱ�BC��(��ͼ1).
(3)��PQ����ABC�ⲿʱ(��ͼ2)����y����x�ĺ�����ϵʽ.(ע��x��ȡֵ��Χ)
���𰸡�(1)4��(2)2.4��(3)y=4x-![]() x2��(2.4<x<6).
x2��(2.4<x<6).
��������
��1�����������ε������ʽ�������ε������![]() ���ס����㼴�ɣ�
���ס����㼴�ɣ�
��2�����ݡ�AMN���ABC���ƣ����������ζ�Ӧ�ߵıȵ������Ʊ���ʽ���㣻
��3�����������ڡ�ABC�ڵı߳�Ϊa��Ҳ���ǡ�ABC�ĸ����������ڵij��ȣ�Ȼ�����ã�2�������㷽���������a�ij��ȣ������þ��ε������ʽ���н��
��1����S��ABC��12��
��![]() BCAD��12����BC��6��
BCAD��12����BC��6��
��AD��4��
��2����AD��MN�ཻ�ڵ�H��
��MN��BC��
���AMN�ס�ABC��
��![]() ��
��
��![]() ��
��
��ã�x��![]()
�൱x��![]() =2.4ʱ������MPQN�ı�Pǡ������BC���ϣ�
=2.4ʱ������MPQN�ı�Pǡ������BC���ϣ�
��3����MP��NQ�ֱ���BC�ཻ�ڵ�E��F����PQ����ABC���ⲿʱ��x��ȡֵΪ2.4��x��6.
��HD��a����AH��4a��
��![]() ��
��
��![]() ��
��
��ã�a��![]() x��4��
x��4��
�߾���MEFN�������MN��HD��
��y��x��![]() x��4����
x��4����![]() x2��4x��2.4��x��6����
x2��4x��2.4��x��6����

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�