题目内容
【题目】![]() 如图
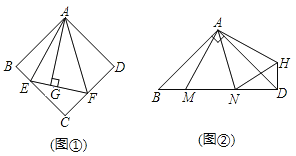
如图![]() ,在正方形ABCD中,
,在正方形ABCD中,![]() 的顶点E,F分别在BC,CD边上,高AG与正方形的边长相等,求
的顶点E,F分别在BC,CD边上,高AG与正方形的边长相等,求![]() 的度数.
的度数.
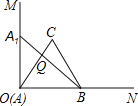
![]() 如图
如图![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,点M,N是BD边上的任意两点,且
,点M,N是BD边上的任意两点,且![]() ,将
,将![]() 绕点A逆时针旋转
绕点A逆时针旋转![]() 至
至![]() 位置,连接NH,试判断MN,ND,DH之间的数量关系,并说明理由.
位置,连接NH,试判断MN,ND,DH之间的数量关系,并说明理由.
![]() 在图
在图![]() 中,连接BD分别交AE,AF于点M,N,若
中,连接BD分别交AE,AF于点M,N,若![]() ,
,![]() ,
,![]() ,求AG,MN的长.
,求AG,MN的长.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
![]() 根据高AG与正方形的边长相等,证明三角形全等,进而证明角相等,从而求出解.
根据高AG与正方形的边长相等,证明三角形全等,进而证明角相等,从而求出解.
![]() 用三角形全等和正方形的对角线平分每一组对角的知识可证明结论.
用三角形全等和正方形的对角线平分每一组对角的知识可证明结论.
![]() 设出线段的长,结合方程思想,用数形结合得到结果.
设出线段的长,结合方程思想,用数形结合得到结果.
解:![]() 在
在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,
![]() ≌
≌![]() .
.
![]() .
.
同理,![]() .
.
![]() .
.
![]() .
.
![]() ,
,![]() ,
,
![]() .
.
![]() .
.
又![]() ,
,![]() ,
,
![]() ≌
≌![]() .
.
![]() .
.
![]() ,
,![]() ,
,
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() 由
由![]() 知,
知,![]() ,
,![]() .
.
设![]() ,则
,则![]() ,
,![]() .
.
在![]() 中,
中,
![]() ,
,
∴(x-4)2+(x-6)2=102
解这个方程,得![]() ,
,![]() 舍去负根
舍去负根![]() .
.
即![]() .
.
在![]() 中,
中,
![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,
![]() .
.
设![]() ,则
,则![]() (
(![]() )2+(
)2+(![]() )2.
)2.
即![]() (
(![]() )2+(
)2+(![]() )2,
)2,
![]() 即
即![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目