��Ŀ����
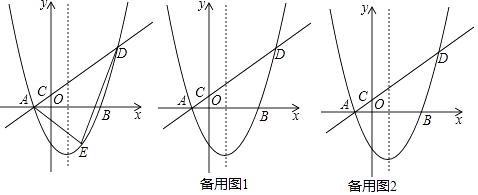
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���M������Ϊ��2��8������N������Ϊ��2��6�������߶�MN����ƽ��4����λ���ȵõ��߶�PQ����P�͵�Q�ֱ��ǵ�M�͵�N�Ķ�Ӧ�㣩������MP��NQ����K���߶�MP���е㣮
��1�����K�����ꣻ
��2����������PMNQ��ÿ��1����λ���ȵ��ٶ������·��˶�������A��B��C��D��E�ֱ��ǵ�M��N��Q��P��K�Ķ�Ӧ�㣩����BC��x���غ�ʱֹͣ�˶�������OA��OE�����˶�ʱ��Ϊt�룬���ú�t��ʽ�ӱ�ʾ������OAE�����S����Ҫ��д��t��ȡֵ��Χ����
��3���ڣ�2���������£�����OB��OD�����Ƿ����ijһʱ��t��ʹ������OBD���������������OAE������������ڣ������tֵ���������ڣ���˵�����ɣ�

���𰸡���1����4��8����2��S��OAE��8��t��3��2���6��
��������
��1������M��N�������ƽ�Ƶ����ʿ�֪��MN��y���PQ������K��PM���е�ɵ�K�����ꣻ
��2�����������������ʽ�ɵ�������OAE�����S��
��3���������������
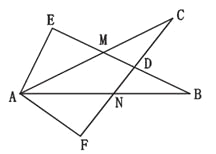
����ͼ2������B��OD�Ϸ�ʱ
����ͼ3������B��OD�Ϸ�ʱ��
����B��BG��x����G����D��DH��x����H���ֱ����������OBD���������������OAE������з��̿ɵý��ۣ�
��1��������ã�PM��4��
��K��PM���е㣬
��MK��2��
�ߵ�M������Ϊ��2��8������N������Ϊ��2��6����
��MN��y�ᣬ
��K��4��8����
��2����ͼ1��ʾ���ӳ�DA��y����F��
��OF��AE��F��0��8��t����
��OF��8��t��
��S��OAE��![]() OFAE��
OFAE��![]() ��8��t����2��8��t��
��8��t����2��8��t��
��3�����ڣ��������������
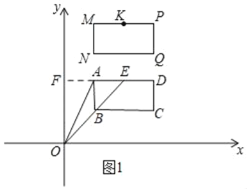
����ͼ2������B��OD�Ϸ�ʱ��

����B��BG��x����G����D��DH��x����H����B��2��6��t����D��6��0����
��OG��2��GH��4��BG��6��t��DH��8��t��OH��6��
S��OBD��S��OBG+S�ı���DBGH+S��ODH��
��![]() OGBG+
OGBG+![]() ��BG+DH��GH��
��BG+DH��GH��![]() OHDH��
OHDH��
��![]() ��2��6-t��+
��2��6-t��+![]() ��4��6��t+8��t����
��4��6��t+8��t����![]() ��6��8��t����
��6��8��t����
��10��2t��
��S��OBD��S��OAE��
��10��2t��8��t��
t��2��
����ͼ3������B��OD�Ϸ�ʱ��
����B��BG��x����G����D��DH��x����H��
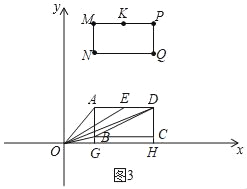
��B��2��6��t����D��6��8��t����
��OG��2��GH��4��BG��6��t��DH��8��t��OH��6��
S��OBD��S��ODH��S�ı���DBGH��S��OBG��
��![]() OHDH��
OHDH��![]() ��BG+DH��GH��
��BG+DH��GH��![]() OGBG��
OGBG��
��![]() ��2��8-t����
��2��8-t����![]() ��4��6��t+8��t����
��4��6��t+8��t����![]() ��2��6��t����
��2��6��t����
��2t��10��
��S��OBD��S��OAE��
��2t��10��8��t��
t��6��
���ϣ�t��ֵ��2���6�룮