题目内容
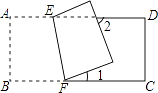
【题目】如图,在△ABC中,∠C=90°,AE是△ABC的角平分线;ED平分∠AEB交AB于点D;∠CAE=∠B.
(1)如果AC=3.5 cm,求AB的长度;
(2)猜想:ED与AB的位置关系,并证明你的猜想。

【答案】(1)7cm;(2) ED⊥AB.理由见解析
【解析】
(1)根据30°角所对的直角边等于斜边的一半得出AB=2AC=7cm;
(2)先由∠EAB=∠B,根据等角对等边得出EB=EA,又ED平分∠AEB,根据等腰三角形三线合一的性质得到ED⊥AB.
解:(1)∵AE是△ABC的角平分线,
∴∠CAE=∠EAB,
∵∠CAE=∠B,
∴∠CAE=∠EAB=∠B.
∵在△ABC中,∠C=90°,
∴∠CAE+∠EAB+∠B=3∠B=90°,
∴∠B=30°;
在△ABC中,∠C=90°,∠B=30°,AC=3.5cm,
∴AB=2AC=7cm;
(2)猜想:ED⊥AB.理由如下:
∵∠EAB=∠B,
∴EB=EA,
∵ED平分∠AEB,
∴ED⊥AB.(三线合一)

练习册系列答案
相关题目