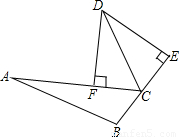
题目内容
(2005•十堰)如图,在△ABC中,∠A=110°,∠B=35°,请你应用变换的方法得到一个三角形使它与△ABC全等,且要求得到的三角形与原△ABC组成一个四边形.(1)要求用两种变换方法解决上述问题;(写出变换名称,画出图形即可)
(2)指出四边形是什么图形?(不要求证明)
说明:如用两种平移变换方法解决此题算一种变换;两种变换是指平移、旋转等不同变换.
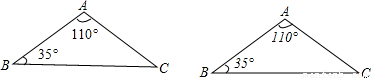
【答案】分析:(1)此题的答案也不唯一,可以平移,旋转,也可以作轴对称图形,这里就做一个以BC为对称轴作对称变换.
(2)△ABC是等腰三角形,以BC所在直线作轴对称图形时,可以得到四边形的四边相等;
以BC的中点为旋转中心作旋转变换时,所得四边形对角线互相平分,即可判断四边形的形状.
解答:解:(1)①以BC为对称轴作对称变换(或以BC的中点O把△ABC绕O点旋转180°)如图一.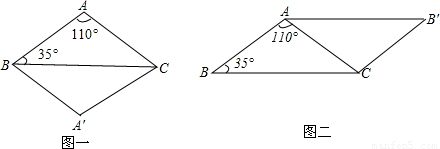
(2分)
②把△ABC绕AC的中点O旋转180°即可(或把△ABC绕AB的中点O旋转180°即可),如图二.
(4分)
(2)分别是菱形和平行四边形.(6分)
点评:本题主要考查了轴对称图形的应用.
(2)△ABC是等腰三角形,以BC所在直线作轴对称图形时,可以得到四边形的四边相等;
以BC的中点为旋转中心作旋转变换时,所得四边形对角线互相平分,即可判断四边形的形状.
解答:解:(1)①以BC为对称轴作对称变换(或以BC的中点O把△ABC绕O点旋转180°)如图一.
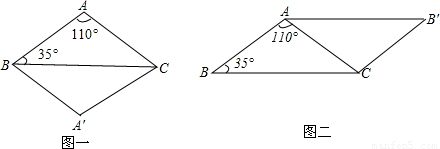
(2分)
②把△ABC绕AC的中点O旋转180°即可(或把△ABC绕AB的中点O旋转180°即可),如图二.
(4分)
(2)分别是菱形和平行四边形.(6分)
点评:本题主要考查了轴对称图形的应用.

练习册系列答案
相关题目
 x+1分别交x轴于E,交y轴于F,问△BDC与△EOF是否有可能全等?如果有可能全等请给出证明;如果不可能全等请说明理由.
x+1分别交x轴于E,交y轴于F,问△BDC与△EOF是否有可能全等?如果有可能全等请给出证明;如果不可能全等请说明理由.
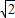 x+1分别交x轴于E,交y轴于F,问△BDC与△EOF是否有可能全等?如果有可能全等请给出证明;如果不可能全等请说明理由.
x+1分别交x轴于E,交y轴于F,问△BDC与△EOF是否有可能全等?如果有可能全等请给出证明;如果不可能全等请说明理由.
 (2005•十堰)如图,l1表示神风摩托车厂一天的销售收入与摩托车销售量的关系;l2表示摩托车厂一天的销售成本与销售量的关系.
(2005•十堰)如图,l1表示神风摩托车厂一天的销售收入与摩托车销售量的关系;l2表示摩托车厂一天的销售成本与销售量的关系. (2005•十堰)如图,l1表示神风摩托车厂一天的销售收入与摩托车销售量的关系;l2表示摩托车厂一天的销售成本与销售量的关系.
(2005•十堰)如图,l1表示神风摩托车厂一天的销售收入与摩托车销售量的关系;l2表示摩托车厂一天的销售成本与销售量的关系.