题目内容
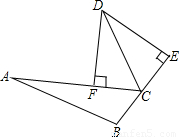
(2005•十堰)如图,已知抛物线y=x2-2x+n与x轴交于不同的两点A,B,其顶点是C,D是抛物线的对称轴与x轴的交点.(1)求实数n的取值范围.
(2)求顶点C的坐标;
(3)求线段AB的长;
(4)若直线y=
 x+1分别交x轴于E,交y轴于F,问△BDC与△EOF是否有可能全等?如果有可能全等请给出证明;如果不可能全等请说明理由.
x+1分别交x轴于E,交y轴于F,问△BDC与△EOF是否有可能全等?如果有可能全等请给出证明;如果不可能全等请说明理由.
【答案】分析:(1)已知抛物线与x轴有两个不同的交点,因此令y=0,得出的方程的△>0,据此可求出n的取值范围.
(2)本题用公式法或配方法求解均可.
(3)可求出A、B的横坐标,进而可得出BA的长(也可用韦达定理求解).
(4)先根据直线的解析式求出OE,OF的长,然后看这两个直角三角形的对应边能否对应相等即可.
解答:解:(1)令y=0,则有:x2-2x+n=0,
依题意有:△=4-4n>0,
∴n<1.
由于抛物线与y轴的交点在y轴正半轴上,
因此0<n<1.
(2)y=x2-2x+n=(x-1)2+n-1,
∴C(1,n-1).
(3)令y=0,x2-2x+n=0,
解得x=1+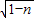 ,x=1-
,x=1-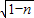 ,
,
∴B(1+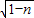 ,0),A(1-
,0),A(1-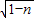 ,0),
,0),
∴AB=2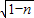 .
.
(4)易知:E(-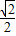 ,0),F(0,1),
,0),F(0,1),
∴OE=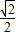 ,OF=1.
,OF=1.
由(2)(3)可得BD=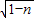 ,CD=1-n,
,CD=1-n,
①当OE=CD时,1-n=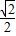 ,
,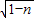 =
= ≠1,因此BD≠OF,
≠1,因此BD≠OF,
∴两三角形不可能全等.
②当OE=BD时,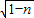 =
=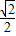 ,1-n=
,1-n= ≠1,因此CD≠OF,
≠1,因此CD≠OF,
∴两三角形不全等.
综上所述,△BDC与△EOF不可能全等.
点评:本题主要考查了二次函数与一元二次方程的关系,全等三角形的判定等知识点.
(2)本题用公式法或配方法求解均可.
(3)可求出A、B的横坐标,进而可得出BA的长(也可用韦达定理求解).
(4)先根据直线的解析式求出OE,OF的长,然后看这两个直角三角形的对应边能否对应相等即可.
解答:解:(1)令y=0,则有:x2-2x+n=0,
依题意有:△=4-4n>0,
∴n<1.
由于抛物线与y轴的交点在y轴正半轴上,
因此0<n<1.
(2)y=x2-2x+n=(x-1)2+n-1,
∴C(1,n-1).
(3)令y=0,x2-2x+n=0,
解得x=1+
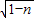 ,x=1-
,x=1-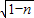 ,
,∴B(1+
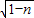 ,0),A(1-
,0),A(1-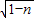 ,0),
,0),∴AB=2
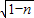 .
.(4)易知:E(-
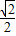 ,0),F(0,1),
,0),F(0,1),∴OE=
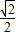 ,OF=1.
,OF=1.由(2)(3)可得BD=
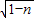 ,CD=1-n,
,CD=1-n,①当OE=CD时,1-n=
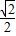 ,
,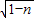 =
= ≠1,因此BD≠OF,
≠1,因此BD≠OF,∴两三角形不可能全等.
②当OE=BD时,
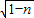 =
=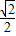 ,1-n=
,1-n= ≠1,因此CD≠OF,
≠1,因此CD≠OF,∴两三角形不全等.
综上所述,△BDC与△EOF不可能全等.
点评:本题主要考查了二次函数与一元二次方程的关系,全等三角形的判定等知识点.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
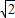 x+1分别交x轴于E,交y轴于F,问△BDC与△EOF是否有可能全等?如果有可能全等请给出证明;如果不可能全等请说明理由.
x+1分别交x轴于E,交y轴于F,问△BDC与△EOF是否有可能全等?如果有可能全等请给出证明;如果不可能全等请说明理由.
 (2005•十堰)如图,l1表示神风摩托车厂一天的销售收入与摩托车销售量的关系;l2表示摩托车厂一天的销售成本与销售量的关系.
(2005•十堰)如图,l1表示神风摩托车厂一天的销售收入与摩托车销售量的关系;l2表示摩托车厂一天的销售成本与销售量的关系. (2005•十堰)如图,l1表示神风摩托车厂一天的销售收入与摩托车销售量的关系;l2表示摩托车厂一天的销售成本与销售量的关系.
(2005•十堰)如图,l1表示神风摩托车厂一天的销售收入与摩托车销售量的关系;l2表示摩托车厂一天的销售成本与销售量的关系.