题目内容
(2005•十堰)如图,D是△ABC外角∠ACE的平分线上一点,DF⊥AC于F,DE⊥BC交延长线于E.(1)求证:CE=CF;
(2)找一点D′,使得DFD′E是菱形,请你画出草图,并简要叙述D′的位置.
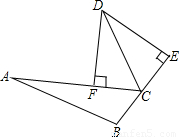
【答案】分析:(1)由已知可得DF=DE.再利用HL判定△DFC≌△DEC,得到CE=CF;
(2)连接EF交DC于点O,延长DC到D′,使OD′=DO.
由△DFC≌△DEC得到∠FDC=∠EDC;根据等腰三角形的三线合一性质得到DC⊥EF,OE=OF;再根据对角线互相垂直平分的四边形是菱形得到四边形DFD’E是菱形.
解答: (1)证明:∵D是△ABC外角∠ACE的平分线上一点,DF⊥AC于F,DE⊥BC交延长线于E,
(1)证明:∵D是△ABC外角∠ACE的平分线上一点,DF⊥AC于F,DE⊥BC交延长线于E,
∴DF=DE.
∵DC=DC′,
∴△DFC≌△DEC.
∴CE=CF.
(2)解:连接EF交DC于点O,延长DC到D′,使OD′=DO.
∵△DFC≌△DEC,
∴∠FDC=∠EDC,
∴DC⊥EF,OE=OF.
∵DO=D′O,
∴四边形DFD’E是菱形.
点评:此题主要考查学生对全等三角形的判定及菱形的判定的理解及掌握.
(2)连接EF交DC于点O,延长DC到D′,使OD′=DO.
由△DFC≌△DEC得到∠FDC=∠EDC;根据等腰三角形的三线合一性质得到DC⊥EF,OE=OF;再根据对角线互相垂直平分的四边形是菱形得到四边形DFD’E是菱形.
解答:
 (1)证明:∵D是△ABC外角∠ACE的平分线上一点,DF⊥AC于F,DE⊥BC交延长线于E,
(1)证明:∵D是△ABC外角∠ACE的平分线上一点,DF⊥AC于F,DE⊥BC交延长线于E,∴DF=DE.
∵DC=DC′,
∴△DFC≌△DEC.
∴CE=CF.
(2)解:连接EF交DC于点O,延长DC到D′,使OD′=DO.
∵△DFC≌△DEC,
∴∠FDC=∠EDC,
∴DC⊥EF,OE=OF.
∵DO=D′O,
∴四边形DFD’E是菱形.
点评:此题主要考查学生对全等三角形的判定及菱形的判定的理解及掌握.

练习册系列答案
相关题目
 x+1分别交x轴于E,交y轴于F,问△BDC与△EOF是否有可能全等?如果有可能全等请给出证明;如果不可能全等请说明理由.
x+1分别交x轴于E,交y轴于F,问△BDC与△EOF是否有可能全等?如果有可能全等请给出证明;如果不可能全等请说明理由.
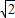 x+1分别交x轴于E,交y轴于F,问△BDC与△EOF是否有可能全等?如果有可能全等请给出证明;如果不可能全等请说明理由.
x+1分别交x轴于E,交y轴于F,问△BDC与△EOF是否有可能全等?如果有可能全等请给出证明;如果不可能全等请说明理由.
 (2005•十堰)如图,l1表示神风摩托车厂一天的销售收入与摩托车销售量的关系;l2表示摩托车厂一天的销售成本与销售量的关系.
(2005•十堰)如图,l1表示神风摩托车厂一天的销售收入与摩托车销售量的关系;l2表示摩托车厂一天的销售成本与销售量的关系. (2005•十堰)如图,l1表示神风摩托车厂一天的销售收入与摩托车销售量的关系;l2表示摩托车厂一天的销售成本与销售量的关系.
(2005•十堰)如图,l1表示神风摩托车厂一天的销售收入与摩托车销售量的关系;l2表示摩托车厂一天的销售成本与销售量的关系.