题目内容
 (2005•十堰)如图,l1表示神风摩托车厂一天的销售收入与摩托车销售量的关系;l2表示摩托车厂一天的销售成本与销售量的关系.
(2005•十堰)如图,l1表示神风摩托车厂一天的销售收入与摩托车销售量的关系;l2表示摩托车厂一天的销售成本与销售量的关系.(1)写出销售收入与销售量之间的函数关系式;
(2)写出销售成本与销售量之间的函数关系式;
(3)当一天的销售量为多少辆时,销售收入等于销售成本;
(4)当一天的销售超过多少辆时,工厂才能获利?(利润=收入-成本)
【答案】分析:(1)设y=kx,根据题意可知当x=4时,y=4,则k=1,即销售收入与销售量之间的函数关系式为y=x;
(2)设y=kx+b,把已知坐标代入可得解析式y= x+2;
x+2;
(3)由图可知当x=4时,销售收入等于销售成本,故x=4;
(4)由图象可知x>4时,工厂才能获利.
解答:解:(1)设y=kx,
∵直线过(4,4)两点,
∴4=4k,
∴k=1,
∴y=x;
(2)设y=kx+b,
∵直线过(0,2)、(4,4)两点,
∴2=b,4=4k+2,
∴k= ,
,
∴y= x+2;
x+2;
(3)由图象知,当x=4时,销售收入等于销售成本,
∴x= x+2,
x+2,
∴x=4;
(4)由图象知:当x>4时,工厂才能获利,
或x-( x+2)>0时,即x>4时,才能获利.
x+2)>0时,即x>4时,才能获利.
点评:本题重点考查了一次函数的图象和性质,也考查了一次函数的应用.此外正确理解题意也是解题的关键.
(2)设y=kx+b,把已知坐标代入可得解析式y=
 x+2;
x+2;(3)由图可知当x=4时,销售收入等于销售成本,故x=4;
(4)由图象可知x>4时,工厂才能获利.
解答:解:(1)设y=kx,
∵直线过(4,4)两点,
∴4=4k,
∴k=1,
∴y=x;
(2)设y=kx+b,
∵直线过(0,2)、(4,4)两点,
∴2=b,4=4k+2,
∴k=
 ,
,∴y=
 x+2;
x+2;(3)由图象知,当x=4时,销售收入等于销售成本,
∴x=
 x+2,
x+2,∴x=4;
(4)由图象知:当x>4时,工厂才能获利,
或x-(
 x+2)>0时,即x>4时,才能获利.
x+2)>0时,即x>4时,才能获利.点评:本题重点考查了一次函数的图象和性质,也考查了一次函数的应用.此外正确理解题意也是解题的关键.

练习册系列答案
相关题目
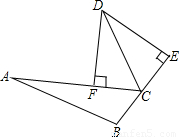
 x+1分别交x轴于E,交y轴于F,问△BDC与△EOF是否有可能全等?如果有可能全等请给出证明;如果不可能全等请说明理由.
x+1分别交x轴于E,交y轴于F,问△BDC与△EOF是否有可能全等?如果有可能全等请给出证明;如果不可能全等请说明理由.
 x+1分别交x轴于E,交y轴于F,问△BDC与△EOF是否有可能全等?如果有可能全等请给出证明;如果不可能全等请说明理由.
x+1分别交x轴于E,交y轴于F,问△BDC与△EOF是否有可能全等?如果有可能全等请给出证明;如果不可能全等请说明理由.
 (2005•十堰)如图,l1表示神风摩托车厂一天的销售收入与摩托车销售量的关系;l2表示摩托车厂一天的销售成本与销售量的关系.
(2005•十堰)如图,l1表示神风摩托车厂一天的销售收入与摩托车销售量的关系;l2表示摩托车厂一天的销售成本与销售量的关系.