题目内容
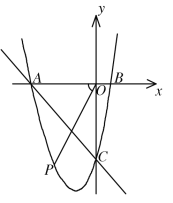
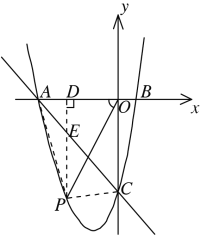
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-4,0)、B(1,0),与y轴交于点C(0,-4),P是直线AC下方抛物线上的点,若△ACP的面积为6,则tan∠AOP的值为_____________
【答案】6或![]() .
.
【解析】
连接PA,PC,过P作PD⊥x轴,与AC交于点E,采用待定系数法求出二次函数与直线AC的解析式,设出P点坐标,求出E点纵坐标,然后采用“铅锤法”表示出△ACP的面积,解方程求出P点坐标,再根据正切的定义即可求解.
如图,连接PA,PC,过P作PD⊥x轴,与AC交于点E,
将A(-4,0),B(1,0),C(0,-4)代入抛物线解析式得,
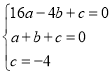 ,解得
,解得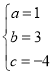
∴二次函数解析式为![]()
设直线AC解析式为![]() ,
,
将A(-4,0),C(0,-4)代入直线解析式得
![]() ,解得
,解得![]()
∴直线AC解析式为![]()
设P点坐标为![]() ,
,
∵PD⊥x轴,
∴E点横坐标为m,
将E点横坐标代入直线AC得![]() ,则E点坐标为
,则E点坐标为![]() ,
,
∴PE=![]()
∴S△ACP=![]() ,
,
解得![]() 或
或![]()
当m=-1时,P点坐标为(-1,-6),tan∠AOP=![]()
当m=-3时,P点坐标为(-3,-4),tan∠AOP=![]()
故答案为:6或![]() .
.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目