题目内容
【题目】如图,将△ABC绕点C顺时针旋转36°,点B的对应点为点E,点A的对应点为点D,此时点E恰好落在边AC上时,连接AD,若AB=BC,AC=2,则AB的长度是( )
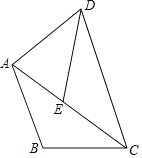
A. ![]() B. 1C.
B. 1C. ![]() D.
D. ![]()
【答案】A
【解析】
首先证明DA=ED=EC,设AB=x,则AD=DE=EC=x,由△DAE∽△CAD,可得AD2=AEAC,由此构建方程即可解决问题.
解:∵AB=BC,∠ACB=36°,
∴∠BAC=∠ACB=36°,∠B=∠CED=108°,
∴∠AED=72°,
∴CA=CD,∠ACD=36°,
∴∠CAD=∠CDA=72°,
∴∠ADE=∠ACD=36°,
∴DA=ED=EC,设AB=x,则AD=DE=EC=x,
∵∠DAE=∠CAD,∠ADE=∠ACD,
∴△DAE∽△CAD,
∴AD2=AEAC,
∴x2=(2﹣x)2,
∴x=![]() ﹣1或﹣
﹣1或﹣![]() ﹣1(舍弃),
﹣1(舍弃),
∴AB=![]() ﹣1,
﹣1,
故选:A.

 名校课堂系列答案
名校课堂系列答案【题目】某公司生产的某种产品每件成本为40元,经市场调查整理出如下信息:
①该产品90天内日销售量(m件)与时间(第x天)满足一次函数关系,部分数据如下表:
时间(第x天) | 1 | 3 | 6 | 10 | … |
日销售量(m件) | 198 | 194 | 188 | 180 | … |
②该产品90天内每天的销售价格与时间(第x天)的关系如下表:
时间(第x天) | 1≤x<50 | 50≤x≤90 |
销售价格(元/件) | x+60 | 100 |
(1)求m关于x的一次函数表达式;
(2)设销售该产品每天利润为y元,请写出y关于x的函数表达式,并求出在90天内该产品哪天的销售利润最大?最大利润是多少?【提示:每天销售利润=日销售量×(每件销售价格-每件成本)】
(3)在该产品销售的过程中,共有多少天销售利润不低于5400元,请直接写出结果.
【题目】铁岭“荷花节”举办了为期15天的“荷花美食”厨艺秀.小张购进一批食材制作特色美食,每盒售价为50元,由于食材需要冷藏保存,导致成本逐日增加,第x天(1≤x≤15且x为整数)时每盒成本为p元,已知p与x之间满足一次函数关系;第3天时,每盒成本为21元;第7天时,每盒成本为25元,每天的销售量为y盒,y与x之间的关系如下表所示:
第x天 | 1≤x≤6 | 6<x≤15 |
每天的销售量y/盒 | 10 | x+6 |
(1)求p与x的函数关系式;
(2)若每天的销售利润为w元,求w与x的函数关系式,并求出第几天时当天的销售利润最大,最大销售利润是多少元?
(3)在“荷花美食”厨艺秀期间,共有多少天小张每天的销售利润不低于325元?请直接写出结果.