题目内容
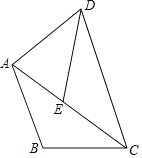
【题目】如图,M、N是边长为6的正方形ABCD的边CD上的两个动点,满足AM=BN,连接AC交BN于点E,连接DE交AM于点F,连接CF.
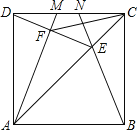
(1)求证:DE=BE;
(2)判断DE与AM的位置关系,并证明;
(3)判断线段CF是否存在最小值?若存在,求出来,若不存在,说明理由.
【答案】(1)见解析;(2)DE⊥AM,见解析;(3)存在最小值,最小值为![]() .
.
【解析】
(1)证明△DAE≌△BAE(SAS)即可解决问题.
(2)想办法证明∠DAM=∠EDC即可.
(3)存在最小值.如图,取AD的中点O,连接OF、OC,利用三角形三边关系解决问题即可.
解:(1)证明:在正方形ABCD中,AD=AB,∠DAE=BAE,又AE为公共边,
∴△DAE≌△BAE(SAS),
∴DE=BE.
(2)结论:互相垂直.
理由::在正方形ABCD中,AD=BC=CD,∠ADC=∠BCD=90°,
∵AM=BN,
∴Rt△ADM≌Rt△BCN(HL),
∴∠DAM=∠CBN
由(1)知DE=BE,又CD=CB,CE为公共边,
∴△DCE≌△BCE(SSS),
∴∠CDE=∠CBE
∵∠ADF+∠CDE=∠ADC=90°
∴∠DAF+∠ADF=90°
∴∠DFA=180°﹣90°=90°
即DE⊥AM.
(3)存在最小值.如图,取AD的中点O,连接OF、OC,
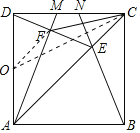
则OF=DO=![]() AD=3,
AD=3,
在Rt△OCD中,
OC=![]() ,
,
根据三角形的三边关系,OF+CF>OC,
∴当O、F、C三点共线时,CF的长度最小,最小值为OC﹣OF=![]() .
.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目