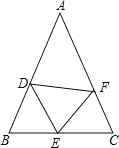
[题目]如图.在△ABC中.AB=AC.DE垂直平分AB．(1)若AB=AC=10cm.BC=6cm.求△BCE的周长,(2)若∠A=40°.求∠EBC的度数．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，在△ABC中，AB=AC，DE垂直平分AB．

（1）若AB=AC=10cm，BC=6cm，求△BCE的周长；

（2）若∠A=40°，求∠EBC的度数．

【答案】（1）16cm；（2）30°.

【解析】

（1）已知DE垂直平分AB，根据线段垂直平分线的性质可得EA=EB，再由△BCE的周长=BC+CE+BE=BC+CE+AE=BC+AC即可求得△BCE的周长；（2）已知AB=AC，∠A=40°，根据等腰三角形的性质及三角形的内角和定理可得∠ABC=∠C=70°，再由EA=EB，∠A=40°，根据等腰三角形的性质可得∠A=∠ABE=40°；由∠EBC=∠ABC-∠ABE即可求得∠EBC的度数．

（1）∵DE垂直平分AB，

∴EA=EB，

∵AB=AC=10cm，BC=6cm，

∴△BCE的周长=BC+CE+BE=BC+CE+AE=BC+AC=10cm+6cm=16cm.

（2）∵AB=AC，∠A=40°，

∴∠ABC=∠C=70°，

∵EA=EB，∠A=40°，

∴∠A=∠ABE=40°，

∴∠EBC=∠ABC-∠ABE=70°-40°=30°.

练习册系列答案

（1）求每辆甲型汽车和乙型汽车的售价；

（2）某公司拟向该店购买甲，乙两种型号的新能源汽车共6辆，购车费不少于130万元，且不超过140万元.则有哪几种购车方案？

【题目】问题再现：

数形结合是一种重要的数学思想方法，借助这种思想方法可将抽象的数学知识变得直观并且具有可操作性.初中数学里的一些代数公式，很多都可以通过表示几何图形面积的方法进行直观推导和解释.

例如：利用图形的几何意义验证完全平方公式.

将一个边长为的正方形的边长增加，形成两个长方形和两个正方形，如图所示：这个图形的面积可以表示成：

或

∴

这就验证了两数和的完全平方公式.

类比解决：

请你类比上述方法，利用图形的几何意义验证平方差公式.

（要求画出图形并写出推理过程）

问题提出：如何利用图形几何意义的方法证明？

如图所示，表示1个1×1的正方形，即：，表示1个2×2的正方形，与恰好可以拼成1个2×2的正方形，因此：、、就可以表示2个2×2的正方形，即：而、、、恰好可以拼成一个的大正方形.

由此可得：.

尝试解决：

请你类比上述推导过程，利用图形的几何意义确定：_______.（要求写出结论并构造图形写出推证过程）.

问题拓广：

请用上面的表示几何图形面积的方法探究：_______.（直接写出结论即可，不必写出解题过程）.

【题目】如图，中，，D，E，F分别为AB，BC，CA上的点，且，．

（1）求证：≌；

（2）若，求的度数．

【题目】平价商场经销的甲、乙两种商品，甲种商品每件售价98元，利润率为40%；乙种商品每件进价80元，售价128元．

（1）甲种商品每件进价为　　元，每件乙种商品利润率为　　．

（2）若该商场同时购进甲、乙两种商品共50件，恰好总进价为3800元，求购进甲、乙两种商品各多少件？

（3）在“元且“期间，该商场只对乙种商品进行如下的优惠促销活动：按下表优惠条件，

打折前一次性购物总金额	优惠措施
少于等于480元	不优惠
超过480元，但不超过680元	其中480元不打折，超过480元的部分给予6折优惠
超过680元	按购物总额给予7．5折优惠