Question

【题目】(1)方法选择

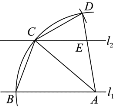
如图①，四边形是的内接四边形，连接，，．求证：.

小颖认为可用截长法证明：在上截取，连接…

小军认为可用补短法证明：延长至点，使得…

请你选择一种方法证明．

(2)类比探究

（探究1）

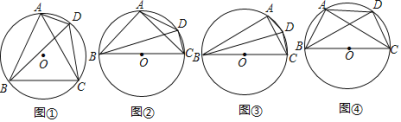
如图②，四边形是的内接四边形，连接，，是的直径，．试用等式表示线段，，之间的数量关系，并证明你的结论．

（探究2）

如图③，四边形是的内接四边形，连接，．若是的直径，，则线段，，之间的等量关系式是______．

(3)拓展猜想

如图④，四边形是的内接四边形，连接，．若是的直径，，则线段，，之间的等量关系式是______．

Answer 1

【答案】(1)方法选择：证明见解析；(2)【探究1】：；【探究2】；(3)拓展猜想：.

【解析】

（1）方法选择：根据等边三角形的性质得到∠ACB=∠ABC=60°，如图①，在BD上截取DM=AD，连接AM，由圆周角定理得到∠ADB=∠ACB=60°，得到AM=AD，根据全等三角形的性质得到BM=CD，于是得到结论；

（2）类比探究：如图②，由BC是⊙O的直径，得到∠BAC=90°，根据等腰直角三角形的性质得到∠ABC=∠ACB=45°，过A作AM⊥AD交BD于M，推出△ADM是等腰直角三角形，求得DM=AD根据全等三角形的性质得到结论；

【探究2】

如图③，根据圆周角定理和三角形的内角和得到∠BAC=90°，∠ACB=60°，过A作AM⊥AD交BD于M，求得∠AMD=30°，根据直角三角形的性质得到MD=2AD，根据相似三角形的性质得到BM=CD，于是得到结论；

（3）如图④，由BC是⊙O的直径，得到∠BAC=90°，过A作AM⊥AD交BD于M，求得∠MAD=90°，根据相似三角形的性质得到BM=CD，DM=AD，于是得到结论．

(1)方法选择：∵，

∴，

如图①，在上截取，连接，

∵，

∴是等边三角形，

∴，

∵，

∵，

∴，

∴，

∴；

(2)类比探究：如图②，

∵是的直径，

∴，

∵，

∴，

过作交于，

∵，

∴是等腰直角三角形，

∴，，

∴，

∴，

∵，

∴，

∴，

∴；

[探究2]如图③，∵若是的直径，，

∴，，

过作交于，

∵，

∴，

∴，

∵，，

∴，

∴，

∴，

∴；

故答案为；

(3)拓展猜想：；

理由：如图④，∵若是的直径，

∴，

过作交于，

∴，

∴，

∴，

∴，

∴，

∵，，

∴，

∴，

∴，

∴.

故答案为.