题目内容
抛物线y＝ax2＋2x＋c与其对称轴相交于点A(1，4)，与x轴正半轴交于点B.
（1）求这条抛物线的函数关系式；
（2）在抛物线对称轴上确定一点C，使△ABC是等腰三角形，求出所有点C的坐标.
（1）y=－x2＋2x＋3；（2）C（1，
），C（1，－4），C（1，
）
解析试题分析：（1）根据题意知，
，求出a=-1.把A（1，4）代入y=-x2+2x+c,得c=3.由此可求出抛物线的解析式；
（2）分别以AB为底和腰进行讨论，从而得出结论.
试题解析：（1）由题意，点A(1，4)即为抛物线的顶点
于是抛物线的对称轴直线x＝，∴a＝－1
抛物线的解析式为y＝－(x－1)2＋4＝－x2＋2x＋3
（2）抛物线与x轴正半轴的交点B的坐标是(3，0)
若点A、B与抛物线对称轴上的点C构成等腰三角形，有三种可能：
当AB＝AC时，点C（1，）
当BA＝BC时，点C（1，－4）
当CA＝CB时，点C（1，）
综上所述，符合要求的点C共有四个.
考点: 二次函数综合题.
练习册系列答案
相关题目
若在国外销售，平均每件产品的利润y2(元)与国外的销售数量t(千件)的关系为： y2=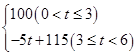
经过点（3,0）,（－1,0）．
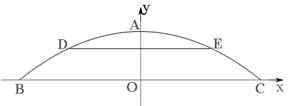
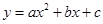经过点A、B和D（4,
）．
时,在抛物线上是否存在点R,使得以点P、B、Q、R为顶点的四边形是平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由．
的图象经过点A（2，－3），B（－1，0）． 
轴只有一个交点，应把图象沿
轴向上平移几个单位？
.