题目内容
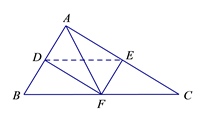
【题目】如图,在△ ![]() 中,点
中,点 ![]() ,
, ![]() ,
, ![]() 分别是边
分别是边 ![]() ,
, ![]() ,
, ![]() 的中点,且
的中点,且 ![]() .
.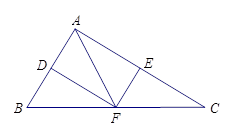
(1)求证:四边形 ![]() 为矩形;
为矩形;
(2)若 ![]() ,
, ![]() ,写出矩形
,写出矩形 ![]() 的周长.
的周长.
【答案】
(1)
证明:连接 ![]() .
.
∵ ![]() ,
, ![]() 分别是边
分别是边 ![]() ,
, ![]() 的中点,
的中点,
∴ ![]() ,
, ![]() .
.
∵点 ![]() 是边
是边 ![]() 的中点,
的中点,
∴ ![]() .
.
∴ ![]()
∴四边形 ![]() 为平行四边形.
为平行四边形.
由点 ![]() ,
, ![]() 分别是边
分别是边 ![]() ,
, ![]() 的中点,可得:
的中点,可得:
![]() .
.
∵ ![]() ,
,
∴ ![]() ,即
,即 ![]() .
.
∴四边形 ![]() 为矩形.
为矩形.
(2)
解:由(1)知四边形ADFE为矩形,
∴ △ABC为RT△,且∠BAC=90°.
∵ F为BC中点,AF=2.
∴BC=4
又∵∠C=30° ,
∴AB=2,
∴AC=![]() =2
=2![]() .
.
∴![]()
【解析】(1)连接 D E,由D、 E 、 F 分别是中点,得到EF∥AD ,AD=EF,根据一组对边平行且相等的四边形为平行四边形. 再根据平行四边形的性质即与已知条件得DE=AF .根据对角线相等的平行四边形为矩形.
(2)由(1)知四边形ADFE为矩形,由矩形性质得△ABC为RT△,且∠BAC=90°.根据直角三角形斜边上的中线等于斜边的一半由AF=2得BC=4.再由∠C=30° ,得AB=2,由勾股定理得AC=![]() =2
=2![]() .从而求出四边形ADFE的周长。
.从而求出四边形ADFE的周长。![]()
【考点精析】根据题目的已知条件,利用三角形中位线定理和平行四边形的判定的相关知识可以得到问题的答案,需要掌握连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.

练习册系列答案
相关题目