题目内容
【题目】如图，在△ABC中，AB＝AC＝5，BC＝6，点D为AB边上的一动点(D不与A、B重合)，过D作DE∥BC，交AC于点E．把△ADE沿直线DE折叠，点A落在点A'处．连结BA'，设AD＝x，△ADE的边DE上的高为y．
(1) 求出y与x的函数关系式；
(2) 若以点A'、B、D为顶点的三角形与△ABC 相似，求x的值；
(3) 当x取何值时，△A' DB是直角三角形．
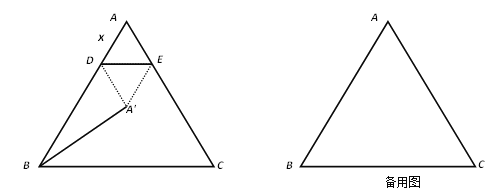
【答案】（1）y＝
(0＜x＜5)．（2）x＝
．（3）当x＝
、x＝
时，△A'DB是直角三角形．
【解析】试题分析：（1）先过A点作AM⊥BC，得出BM=
BC=3，再根据DE∥BC，得出AN⊥DE，即y=AN，再在Rt△ABM中，求出AM的值，再根据DE∥BC，求出△ADE∽△ABC，即可求出y与x的函数关系式；
（2）根据△A'DE由△ADE折叠得到，得出AD=A'D，AE=A'E，再由（1）可得△ADE是等腰三角形，得出AD=A'D，AE=A'E，即可证出四边形ADA'E是菱形，得出∠BDA'=∠BAC，再根据∠BAC≠∠ABC，∠BAC≠∠C，得出∠BDA'≠∠ABC，∠BDA'≠∠C，从而证出△BDA'∽△BAC，即可求出x的值；
（3）先分三种情况进行讨论；第一种情况当∠BDA′=90°，得出∠BDA'≠90°；第二种情况当∠BA'D=90°，根据∠BAM＜90°，∠BA'D＜∠BAM，可得∠BA'D≠90°；第三种情况当∠A'BD=90°，根据∠A'BD=90°，∠AMB=90°，得出△BA'M∽△ABM，即可求出BA′的值，再在Rt△DBA'中，根据DB2+A'B2=A'D2，求出x的值，即可证出△A′DB是直角三角形；
试题解析：（1）如图1，过A点作AM⊥BC，垂足为M，交DE于N点，则BM=
BC=3，
∵DE∥BC，
∴AN⊥DE，即y=AN．
在Rt△ABM中，AM=
=4，
∵DE∥BC，
∴△ADE∽△ABC，
∴
，
∴
，
∴y=
（0＜x＜5）．
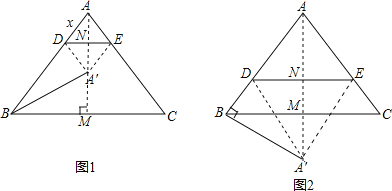
（2）∵△A'DE由△ADE折叠得到，
∴AD=A'D，AE=A'E，
∵由（1）可得△ADE是等腰三角形，
∴AD=AE，
∴A'D=A'E，
∴四边形ADA'E是菱形，
∴AC∥DA'，
∴∠BDA'=∠BAC，
又∵∠BAC≠∠ABC，
∴∠BDA'≠∠ABC，
∵∠BAC≠∠C，
∴∠BDA'≠∠C，
∴有且只有当BD=A'D时，△BDA'∽△BAC，
∴当BD=A'D，即5-x=x时，x=
.
（3）第一种情况：∠BDA'=90°，
∵∠BDA'=∠BAC，而∠BAC≠90°，
∴∠BDA'≠90°．
第二种情况：∠BA'D=90°，
∵在Rt△BA'D中，DB2-A'D2=A'B2，
在Rt△BA'M中，A'M2+BM2=A'B2，
∴DB2-A'D2=A'M2+BM2，
∴（5-x）2-x2=（4-
x）2+（3）2，
解得x=
；
第三种情况：∠A'BD=90°，
∵∠A'BD=90°，∠AMB=90°，
∴△BA'M∽△ABM，
即
，
∴BA'=
，
在Rt△DBA'中，DB2+A'B2=A'D2，
（5-x）2+
=x2，
解得：x=
．
综上可知当x=
或
时，△A'DB是直角三角形．
