题目内容
【题目】如图,矩形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(3,2).点D、E分别在AB、BC边上,BD=BE=1.沿直线DE将△BDE翻折,点B落在点B′处.则点B′的坐标为_____.
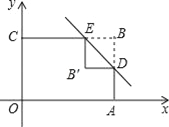
【答案】(2,1).
【解析】由四边形OABC是矩形,BE=BD=1,易得△BED是等腰直角三角形,由折叠的性质,易得∠BEB′=∠BDB′=90°,又由点B的坐标为(3,2),即可求得点B′的坐标.
解:∵四边形OABC是矩形,
∴∠B=90°,
∵BD=BE=1,
∴∠BED=∠BDE=45°,
∵沿直线DE将△BDE翻折,点B落在点B′处,
∴∠B′ED=∠BED=45°,∠B′DE=∠BDE=45°,B′E=BE=1,B′D=BD=1,
∴∠BEB′=∠BDB′=90°,
∵点B的坐标为(3,2),
∴点B′的坐标为(2,1).
故答案为:(2,1).
“点睛”此题考查了折叠的性质、矩形的性质以及坐标与图形的性质.此题难度适中,注意掌握折叠前后图形的对应关系,注意数形结合思想的应用.

练习册系列答案
相关题目