��Ŀ����
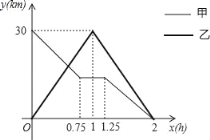
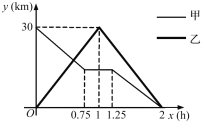
����Ŀ����һ����ֱ�Ĺ�·����A��B����.�ס�������ͬʱ����������綯����A������ǰ��B�أ����ߵ�һ��·��ʱ���ֹ��Ϻ�ͣ��ά��,�ó�����ԭ��������ʻ��B�أ�����Ħ�г���B������ǰ��A�أ�����A�غ�������ԭ·ԭ�����أ��������ͬʱ��B��.�ס���������B�صľ���y(km)������ʻʱ��x(h)֮��ĺ���ͼ����ͼ��ʾ.
��1�������ǰ���ٶ�.
��2����ס��ҵ�һ��������ʱ��.
��3��������֮��ľ��벻����10kmʱ���ܹ������߶Խ���������ϵ����ֱ��д�������н����������߶Խ�����ױ�����ϵ��xȡֵ��Χ.
���𰸡���1������ǰ���ٶ�Ϊ20km/h����2���ס��ҵ�һ���������ڳ�����0.6Сʱ����3��![]() ��
��![]() ��
��
��������
��1���ɺ���ͼ������������ʻ��ʱ�䣬�Ϳ�����·����ʱ���������ʻ���ٶȣ�
��2�������������������ϵֱ��������ۣ�
��3���������ǰy��x֮��ĺ�����ϵʽΪy��1��kx+b����������y��x֮��ĺ�����ϵʽΪy��2��k3x+b3����ǰ��A�صľ���y��km��������ʻʱ��x��h��֮��Ĺ�ϵʽΪy��1��k1x�����ҷ���B�ؾ���B�صľ���y��km��������ʻʱ��x��h��֮��Ĺ�ϵʽΪy��2��k2x+b2���ɴ���ϵ�����������ʽ��������ʽ�������⼴�ɣ�
��1�������⣬��
30��(2-![]() )=20��km/h����
)=20��km/h����
�����ǰ���ٶ�Ϊ20km/h��
��2���ɺ���ͼ��
��30+20��x��30��
���x��0.6��
��ס��ҵ�һ���������ڳ�����0.6Сʱ��
��3���������ǰy��x֮��ĺ�����ϵʽΪy��1��kx+b�������⣬��
![]() ��
��
��ã�![]() ��
��
y��1����20x+30��
���������y��x֮��ĺ�����ϵʽΪy��2��k3x+b3�������⣬��
 ��
��
��ã� ��
��
��y��2����20x+40��
����ǰ��A�صľ���y��km��������ʻʱ��x��h��֮��Ĺ�ϵʽΪy��1��k1x�������⣬��
30��k1��
��y��1��30x��
���ҷ���B�ؾ���B�صľ���y��km��������ʻʱ��x��h��֮��Ĺ�ϵʽΪy��2��k2x+b2�������⣬��
 ��
��
��ã� ��
��
��y����30x+60��
��![]() ʱ��
ʱ��
��![]() ��
��
![]() ��
��
��ã�![]() ��
��
��![]() ��
��![]() ��
��