题目内容
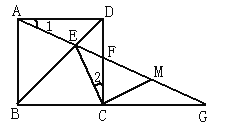
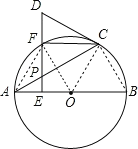
【题目】如图,AB是⊙O的直径,点P是弦AC上一动点(不与A,C重合),过点P作PE⊥AB,垂足为E,射线EP交弧AC于点F,交过点C的切线于点D.
(1)求证:DC=DP;
(2)若∠CAB=30°,当F是弧AC的中点时,判断以A,O,C,F为顶点的四边形是什么特殊四边形?说明理由.
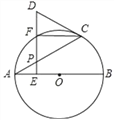
【答案】(1)证明见解析;(2)以A,O,C,F为顶点的四边形是菱形,理由见解析.
【解析】分析:(1)连接OC,根据切线的性质和PE⊥OE以及∠OAC=∠ACO,得∠APE=∠DPC,然后结合对顶角的性质可证得结论;
(2)由![]() 易得△OBC为等边三角形,可得
易得△OBC为等边三角形,可得![]() 由F是
由F是![]() 的中点,易得△AOF与△COF均为等边三角形,可得AF=AO=OC=CF,易得四边形OACF为菱形.
的中点,易得△AOF与△COF均为等边三角形,可得AF=AO=OC=CF,易得四边形OACF为菱形.
详解:(1)证明:连接OC,
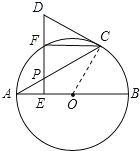
∵∠OAC=∠ACO,PE⊥OE,OC⊥CD,
∴∠APE=∠PCD,
∵∠APE=∠DPC,
∴∠DPC=∠PCD,
∴DC=DP;
(2)以A,O,C,F为顶点的四边形是菱形;
∵![]()
∴△OBC为等边三角形,
∴![]()
连接OF,AF,
∵F是![]() 的中点,
的中点,
∴![]()
∴△AOF与△COF均为等边三角形,
∴AF=AO=OC=CF,
∴四边形OACF为菱形.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目