题目内容
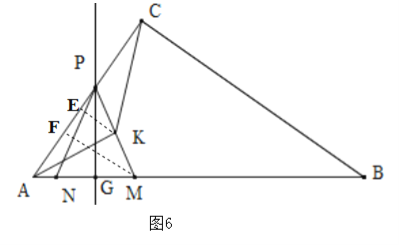
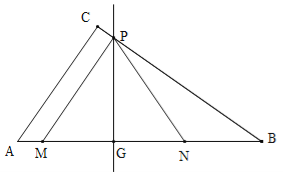
【题目】如图,在Rt△ABC中,∠ACB=900,AC=6,BC=8.动点M从点A出发,以每秒1个单位长度的速度沿AB向点B匀速运动;同时,动点N从点B出发,以每秒3个单位长度的速度沿BA向点A匀速运动.过线段MN的中点G作边AB的垂线,垂足为点G,交△ABC的另一边于点P,连接PM、PN,当点N运动到点A时,M、N两点同时停止运动,设运动时间为t秒.
(1)当t= 秒时,动点M、N相遇;
(2)设△PMN的面积为S,求S与t之间的函数关系式;
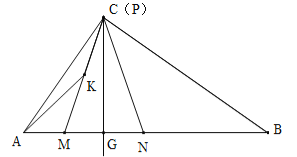
(3)取线段PM的中点K,连接KA、KC,在整个运动过程中,△KAC的面积是否变化?若变化,直接写出它的最大值和最小值;若不变化,请说明理由.
【答案】(1)![]() ;(2)S=
;(2)S=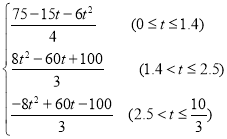 ;(3)在整个运动过程中,△KAC的面积会发生变化,最小值为
;(3)在整个运动过程中,△KAC的面积会发生变化,最小值为![]() ,最大值为4.
,最大值为4.
【解析】
试题分析:(1)由∠ACB=900,AC=6,BC=8,得到AB=10,当M、N相遇时,AM+BN=AB=10,即![]() ,解得
,解得![]() ;
;
(2)由于N比M运动的速度快,故P先在BC上运动,然后在CA上运动.先算出当P与C重合时,所用的时间![]() ,由于相遇的时间
,由于相遇的时间![]() ,停止的时间
,停止的时间![]() ,故分三种情况讨论,
,故分三种情况讨论,
①当![]() 时,M在N的左边,P先在BC上向C靠近;②当
时,M在N的左边,P先在BC上向C靠近;②当![]() 时,M在N的左边,在AC上逐渐远离C;③当
时,M在N的左边,在AC上逐渐远离C;③当![]() 时,M在N的右边,在AC上逐渐远离C.由于S=
时,M在N的右边,在AC上逐渐远离C.由于S=![]() =
=![]() MNPG,MN=10-4t,只需要表示出三种情况中的PG即可,用三角函数计算比较简单;
MNPG,MN=10-4t,只需要表示出三种情况中的PG即可,用三角函数计算比较简单;
(3)分两种情况讨论,①当P在BC上运动时,如图4,当P与C重合时,![]() 最小,当t=0是,M与A重合,N与B重合,如图5,此时三角形
最小,当t=0是,M与A重合,N与B重合,如图5,此时三角形![]() 最大;②当P在CA上运动时,如图6,过K作KE⊥AC于E,过M作MF⊥AC于F,可以得到
最大;②当P在CA上运动时,如图6,过K作KE⊥AC于E,过M作MF⊥AC于F,可以得到![]() =
=![]() ,而
,而![]() ,故当
,故当![]() 时,
时,![]() 的最小值=
的最小值=![]() ,当
,当![]() 时,
时,![]() 的最大值=
的最大值=![]() .综合①②可得到结论.
.综合①②可得到结论.
试题解析:(1)∵∠ACB=900,AC=6,BC=8,∴AB=10,当M、N相遇时,有![]() ,∴
,∴![]() ;
;
(2)∵N比M运动的速度快,∴P先在BC上运动,然后在CA上运动.当P与C重合时,∵![]() =
=![]() ACBC=
ACBC=![]() ABGC,∴GC=6×8÷10=4.8,∴AG=
ABGC,∴GC=6×8÷10=4.8,∴AG=![]() =3.6,∴BG=10-3.6=6.4,∵AM=t,BN=3t,∴MN=10-4t,MG=GN=
=3.6,∴BG=10-3.6=6.4,∵AM=t,BN=3t,∴MN=10-4t,MG=GN=![]() MN=
MN=![]() =
=![]() ,∴
,∴![]() ,∴
,∴![]() .
.
①当![]() 时,M在N的左边,P先在BC上向C靠近,如图1,
时,M在N的左边,P先在BC上向C靠近,如图1,

∵AM=t,BN=3t,∴MN=10-4t,MG=GN=![]() MN=
MN=![]() =
=![]() ,∴GB=GN+NB=
,∴GB=GN+NB=![]() =
=![]() ,∵tanB=
,∵tanB=![]() ,∴
,∴![]() ,∴PG=
,∴PG=![]() ,∴S=
,∴S=![]() =
=![]() MNPG= GNPG=
MNPG= GNPG=![]() =
=![]() ;
;
②当![]() 时,M在N的左边,在AC上逐渐远离C,如图2,
时,M在N的左边,在AC上逐渐远离C,如图2,

由①可知,GN=MG=![]() ,AM=t,∴AG=MG+AM=
,AM=t,∴AG=MG+AM=![]() ,tanA=
,tanA=![]() ,∴
,∴![]() ,∴PG=
,∴PG=![]() ,∴S=
,∴S=![]() =
=![]() MNPG= GNPG=
MNPG= GNPG=![]() =
=![]() ;
;
③当![]() 时,M在N的右边,在AC上逐渐远离C,如图3.
时,M在N的右边,在AC上逐渐远离C,如图3.

MN=NB+AM-AB=![]() =
=![]() ,GN=MG=
,GN=MG=![]() ,AM=t,∴AG= AM-MG =
,AM=t,∴AG= AM-MG =![]() =
=![]() ,tanA=
,tanA=![]() ,∴
,∴![]() ,∴PG=
,∴PG=![]() ,∴S=
,∴S=![]() =
=![]() MNPG= GNPG=
MNPG= GNPG=![]() =
=![]() ;
;
∴S=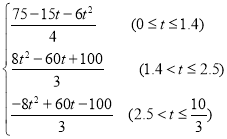 ;
;
(3)①当P在BC上运动时,如图4,当P与C重合时,![]() 最小,过M作MF⊥AC于F,则MF∥BC,∴
最小,过M作MF⊥AC于F,则MF∥BC,∴![]() ,,∴
,,∴![]() ,∴MF=1.12,∴
,∴MF=1.12,∴![]() =
=![]()
![]() =
=![]()
![]() ACMF=
ACMF=![]() =
=![]() ,当t=0是,M与A重合,N与B重合,此时三角形
,当t=0是,M与A重合,N与B重合,此时三角形![]() 最大,如图5,此时BG=AG=5,cosB=
最大,如图5,此时BG=AG=5,cosB=![]() ,∴
,∴![]() ,∴PB=
,∴PB=![]() ,∴PC=BC-PB=8-
,∴PC=BC-PB=8-![]() =
=![]() ,∴
,∴![]() =
=![]() ACPC=
ACPC=![]() =
=![]() ,∵K是AP 的中点,∴
,∵K是AP 的中点,∴![]() =
=![]()
![]() =
=![]() ,∴当P在BC上运动时,△KAC面积的最小值为
,∴当P在BC上运动时,△KAC面积的最小值为![]() ,最大值为
,最大值为![]() ;
;
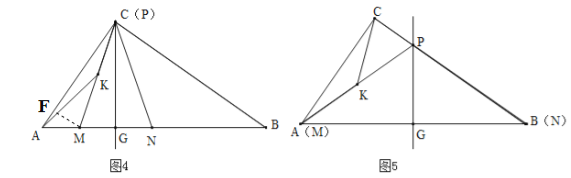
②当P在CA上运动时,如图6,过K作KE⊥AC于E,过M作MF⊥AC于F,∴EK∥FM,∵K为PM的中点,∴EK=![]() FM,∵FM⊥AC,CB⊥AC,∴FM∥CB,∴
FM,∵FM⊥AC,CB⊥AC,∴FM∥CB,∴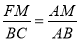 ,∴
,∴![]() ,∴FM=
,∴FM=![]() ,∴EK=
,∴EK=![]() FM=
FM=![]() ,∴
,∴![]() =
=![]() ACEK=
ACEK=![]() =
=![]() ,∵
,∵![]() ,∴当
,∴当![]() 时,
时,![]() 的最小值=
的最小值=![]() ,当
,当![]() 时,
时,![]() 的最大值=
的最大值=![]() .∴当P在CA上运动时,△KAC面积的最小值为
.∴当P在CA上运动时,△KAC面积的最小值为![]() ,最大值为4.
,最大值为4.
综合①②可得:在整个运动过程中,△KAC的面积会发生变化,最小值为![]() ,最大值为4.
,最大值为4.