题目内容
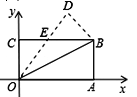
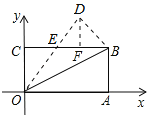
【题目】如图,在矩形OABC中,OA=8,OC=4,沿对角线OB折叠后,点A与点D重合, OD与BC交于点E,设点D的坐标是![]() ,则
,则![]() 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】矩形ABCD中,OA=8,OC=4,∴BC=OA=8,AB=OC=4,由折叠得到OD=OA=BC,∠AOB=∠DOB,∠ODB=∠BAO=90°,在Rt△CBP和Rt△DOB中,∵CB=DO,OB=BO,∴Rt△CBP≌Rt△DOB(HL),∴∠CBO=∠DOB,∴OE=EB,设CE=x,则EB=OE=8﹣x,在Rt△COE中,根据勾股定理得: ![]() ,解得x=3,∴CE=3,OE=5,DE=3,过D作DF⊥BC,可得△COE∽△FDE,∴
,解得x=3,∴CE=3,OE=5,DE=3,过D作DF⊥BC,可得△COE∽△FDE,∴![]() ,即
,即![]() ,解得:DF=
,解得:DF=![]() ,EF=
,EF= ![]() ,∴DF+OC=
,∴DF+OC=![]() =
=![]() ,CF=
,CF=![]() =
=![]() ,则D(
,则D(![]() ,
, ![]() ),所以
),所以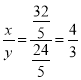 ,故选D.
,故选D.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目