题目内容
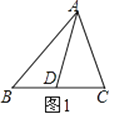
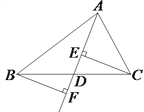
【题目】如图,分别过点C、B作△ABC的BC边上的中线AD及其延长线的垂线, 垂足分别为E、F.求证:BF=CE.
【答案】见解析
【解析】试题分析:由已知条件“过点C、B作AD及其延长线的垂线”易证两个直角相等;再由AD是中线知BD=CD,对顶角∠BDF与∠CDE相等,利用“AAS”来证明△BDF≌△CDE;最后根据全等三角形的对应边相等来证明BF=CE.
证明:根据题意,知CE⊥AF,BF⊥AF,
∴∠CED=∠BFD=90°,
又∵AD是边BC上的中线,
∴BD=DC;
在Rt△BDF和Rt△CDE中,
∠BDF=∠CDE(对顶角相等),BD=CD,∠CED=∠BFD,
∴△BDF≌△CDE(AAS),
∴BF=CE(全等三角形的对应边相等).

练习册系列答案
相关题目