题目内容
【题目】如图,△ABC中,AB=AC,点D是BC上一点,DE⊥AB于E,FD⊥BC于D,G是FC的中点,连接GD.求证:GD⊥DE. 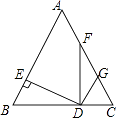
【答案】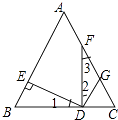 证明:∵AB=AC,
证明:∵AB=AC,
∴∠B=∠C,
∵DE⊥AB,FD⊥BC,
∴∠BED=∠FDC=90°,
∴∠1+∠B=90°,∠3+∠C=90°,
∴∠1=∠3,
∵G是直角三角形FDC的斜边中点,
∴GD=GF,
∴∠2=∠3,
∴∠1=∠2,
∵∠FDC=∠2+∠4=90°,
∴∠1+∠4=90°,
∴∠2+∠FDE=90°,
∴GD⊥DE.
【解析】由∠1+∠EDF=90°可知,只要证明∠1=∠3,∠2=∠3,推出∠1=∠2即可解决问题.
【考点精析】掌握等腰三角形的性质和直角三角形斜边上的中线是解答本题的根本,需要知道等腰三角形的两个底角相等(简称:等边对等角);直角三角形斜边上的中线等于斜边的一半.

练习册系列答案
相关题目