题目内容
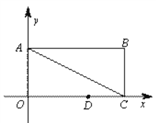
【题目】《九章算术》是我国古代数学名著，有题译文如下：今有门，不知其高宽；有竿，不知其长短．横放，竿比门宽长出4尺；竖放，竿比门高长出2尺；斜放，竿与门对角线长恰好相等．问门高、宽和对角线的长各是多少？设门对角线的长为x尺，下列方程符合题意的是（ ）
A.(x＋2)2＋(x－4)2＝x2B.(x－2)2＋(x－4)2＝x2
C.x2＋(x－4)2＝(x－4)2D.(x－2)2＋x2＝(x＋4)2
【答案】B
【解析】
根据题意表示出门的宽和高，根据勾股定理列出方程即可．
设门对角线的长为x尺，则门的宽为（x－4）尺，高为（x－2）尺，根据题意得：
(x－2)2＋(x－4)2＝x2
故选：B
练习册系列答案
全程金卷系列答案
相关题目
