Question

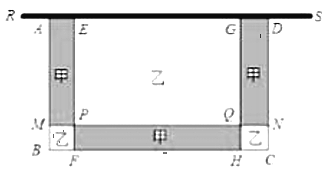
【题目】将一个边长为4的正方形分割成如图所示的9部分，其中，，，全等，，，，也全等，中间小正方形的面积与面积相等，且是以为底的等腰三角形，则的面积为（ ）

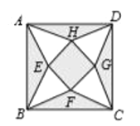
A.2B.C.D.

Answer 1

【答案】C

【解析】

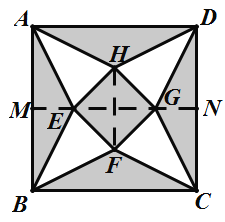
解：如图，连结EG并向两端延长分别交AB、CD于点M、N，连结HF，

∵四边形为正方形，

∴，

∵是以为底的等腰三角形，

∴，则点E在AB的垂直平分线上，

∵≌，

∴为等腰三角形，

∴，则点G在CD的垂直平分线上，

∵四边形为正方形，

∴AB的垂直平分线与CD的垂直平分线重合，

∴即为AB或CD的垂直平分线，

则，，

∵正方形的边长为4，即，

∴，

设，则，

∵正方形的面积与面积相等，

即，解得：，

∵不符合题意，故舍去，

∴，则S正方形EFGH，

∵，，，全等，

∴，

∵正方形的面积，，，，也全等，

∴S正方形ABCD S正方形EFGH ，

故选：C．