МвДҝДЪИЭ
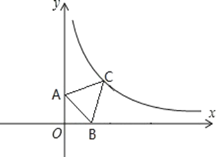
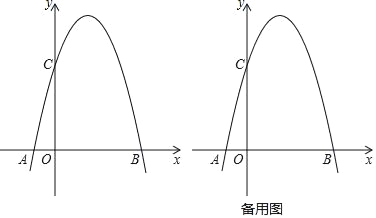
ЎҫМвДҝЎҝДіРЈТ»ГжЗҪ![]() З°УРТ»ҝйҝХөШЈ¬РЈ·ҪЧјұёУГіӨ
З°УРТ»ҝйҝХөШЈ¬РЈ·ҪЧјұёУГіӨ![]() өДХӨАёЈЁ
өДХӨАёЈЁ![]() Ј©О§іЙТ»ёцТ»ГжҝҝЗҪөДіӨ·ҪРО»ЁО§Ј¬ФЩҪ«іӨ·ҪРО
Ј©О§іЙТ»ёцТ»ГжҝҝЗҪөДіӨ·ҪРО»ЁО§Ј¬ФЩҪ«іӨ·ҪРО![]() ·ЦёоіЙБщҝйЈЁИзНјЛщКҫЈ© Ј¬ТСЦӘ
·ЦёоіЙБщҝйЈЁИзНјЛщКҫЈ© Ј¬ТСЦӘ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬Йи
Ј¬Йи![]() Ј®
Ј®
ЈЁ1Ј©УГә¬![]() өДҙъКэКҪұнКҫЈә
өДҙъКэКҪұнКҫЈә![]() Ј»
Ј»![]() Ј®
Ј®
ЈЁ2Ј©өұіӨ·ҪРО![]() өДГж»эөИУЪ
өДГж»эөИУЪ![]() КұЈ¬Зу
КұЈ¬Зу![]() өДіӨЈ®
өДіӨЈ®
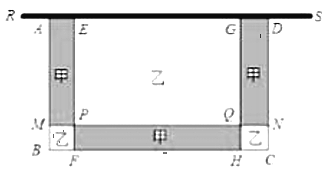
ЈЁ3Ј©ИфФЪИзНјөДјЧЗшУтЦЦЦІ»Ё»ЬЈ®ТТЗшУтЦЦ°ШІЭЖәЈ¬ЦЦ°Ш»Ё»ЬөДіЙұҫОӘГҝЖҪ·ҪГЧ100ФӘЈ¬ЦЦұ»ІЭЖәөДіЙұҫОӘГҝЖҪ·ҪГЧ50ФӘЈ¬ИфЦЦЦІ»Ё»ЬУлІЭЖәөДЧЬ·СУГі¬№э6300ФӘЈ¬Зу»ЁО§өДҝн![]() өД·¶О§Ј®
өД·¶О§Ј®
Ўҫҙр°ёЎҝЈЁ1Ј©![]() Ј»ЈЁ2Ј©ABөДіӨОӘ
Ј»ЈЁ2Ј©ABөДіӨОӘ![]() »т
»т![]() Ј»ЈЁ3Ј©»ЁЖФөДҝн
Ј»ЈЁ3Ј©»ЁЖФөДҝн![]() КұЈ¬ЧЬ·СУГі¬№э 6300 ФӘЈ®
КұЈ¬ЧЬ·СУГі¬№э 6300 ФӘЈ®
ЎҫҪвОцЎҝ
ЈЁ1Ј©ёщҫЭҫШРОөДРФЦКҝЙөГ![]() Ј¬ёщҫЭХӨАёөДЧЬіӨУлҫШРОұЯіӨөД№ШПөјҙҝЙұнКҫіц
Ј¬ёщҫЭХӨАёөДЧЬіӨУлҫШРОұЯіӨөД№ШПөјҙҝЙұнКҫіц![]() Ј¬Ҫш¶шұнКҫіц
Ј¬Ҫш¶шұнКҫіц![]() Ј»
Ј»
ЈЁ2Ј©ПИұнКҫіціӨ·ҪРО![]() өДұЯіӨЈ¬АыУГіӨ·ҪРОөДГж»э№«КҪБРіц·ҪіМЈ¬ЗуҪвјҙҝЙЗуөГABөДіӨЈ»
өДұЯіӨЈ¬АыУГіӨ·ҪРОөДГж»э№«КҪБРіц·ҪіМЈ¬ЗуҪвјҙҝЙЗуөГABөДіӨЈ»
ЈЁ3Ј©ПИЗуіцјЧЗшУтәНТТЗшУтөДГж»эЈ¬ЙиЧЬ·СУГОӘ![]() ФӘЈ¬ТАМвТвБРіцy№ШУЪxөД№ШПөКҪЈ¬АыУГ¶юҙОәҜКэөДРФЦКЗуҪвІ»өИКҪЈ¬јҙҝЙЗуөГ»ЁО§өДҝн
ФӘЈ¬ТАМвТвБРіцy№ШУЪxөД№ШПөКҪЈ¬АыУГ¶юҙОәҜКэөДРФЦКЗуҪвІ»өИКҪЈ¬јҙҝЙЗуөГ»ЁО§өДҝн![]() өД·¶О§Ј®
өД·¶О§Ј®
ҪвЈәЈЁ1Ј©ЎЯЛДұЯРО![]() КЗҫШРОЈ¬
КЗҫШРОЈ¬![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
УЙМвТвөГЈә![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
ЎЯ![]() Ј¬
Ј¬![]() Ј¬Фт
Ј¬Фт![]() Ј¬
Ј¬
ЎаЛДұЯРО![]() КЗЖҪРРЛДұЯРОЈ¬
КЗЖҪРРЛДұЯРОЈ¬
ЎЯ![]() Ј¬
Ј¬
ЎаЛДұЯРО![]() КЗҫШРОЈ¬
КЗҫШРОЈ¬
ЎЯ![]() Ј¬
Ј¬
ЎаЛДұЯРО![]() КЗХэ·ҪРОЈ¬Фт
КЗХэ·ҪРОЈ¬Фт![]() Ј¬
Ј¬
Н¬АнөГЈәЎаЛДұЯРО![]() КЗХэ·ҪРОЈ¬Фт
КЗХэ·ҪРОЈ¬Фт![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
№Кҙр°ёОӘЈә![]() Ј»
Ј»![]() Ј»
Ј»
ЈЁ2Ј©ЎЯ![]() Ј¬
Ј¬
УЙМвТвҝЙөГЈә![]()
ҪвөГЈә![]() Ј¬
Ј¬
![]() өДіӨОӘ
өДіӨОӘ![]() »т
»т![]() Ј»
Ј»
ЈЁ3Ј©јЧЗшУтөДГж»э![]() Ј¬
Ј¬
ТТЗшУтөДГж»э=![]() Ј¬
Ј¬
ЙиЧЬ·СУГОӘ![]() ФӘЈ¬УЙМвТвөГЈә
ФӘЈ¬УЙМвТвөГЈә
![]() Ј¬
Ј¬
ХыАнөГЈә![]() Ј¬
Ј¬
Бо![]() Ј¬јҙ
Ј¬јҙ![]() Ј¬
Ј¬
ҪвөГЈә![]() Ј¬
Ј¬
УЙ¶юҙОәҜКэөДНјПуУлРФЦКҝЙөГЈәөұ ![]() КұЈ¬
КұЈ¬![]() Ј¬
Ј¬
Ўа»ЁЖФөДҝн![]() КұЈ¬ЧЬ·СУГі¬№э 6300 ФӘЈ®
КұЈ¬ЧЬ·СУГі¬№э 6300 ФӘЈ®
ҙрЈәИфЦЦЦІ»Ё»ЬУлІЭЖәөДЧЬ·СУГі¬№э6300ФӘЈ¬»ЁО§өДҝн![]() өД·¶О§ОӘ
өД·¶О§ОӘ![]() Ј®
Ј®

 ФД¶БҝміөПөБРҙр°ё
ФД¶БҝміөПөБРҙр°ёЎҫМвДҝЎҝОӘБЛҙУРЎ»ӘәНРЎБББҪИЛЦРСЎ°ОТ»ИЛІОјУЙд»чұИИьЈ¬ПЦ¶ФЛыГЗөДЙд»чЛ®ЖҪҪшРРІвКФЈ¬БҪИЛФЪПаН¬МхјюПВёчЙд»ч6ҙОЈ¬ГьЦРөД»·КэИзПВЈЁөҘО»Јә»·Ј©Јә
РЎ»ӘЈә7Ј¬8Ј¬7Ј¬8Ј¬9Ј¬9Ј» РЎББЈә5Ј¬8Ј¬7Ј¬8Ј¬10Ј¬10Ј®
ЈЁ1Ј©МоРҙПВұнЈә
ЖҪҫщКэЈЁ»·Ј© | ЦРО»КэЈЁ»·Ј© | ·ҪІоЈЁ»·2Ј© | |
РЎ»Ә | 8 | ||
РЎББ | 8 | 3 |
ЈЁ2Ј©ёщҫЭТФЙПРЕПўЈ¬ДгИПОӘҪМБ·»бСЎФсЛӯІОјУұИИьЈ¬АнУЙКЗКІГҙЈҝ
ЈЁ3Ј©ИфРЎББФЩЙд»ч2ҙОЈ¬·ЦұрГьЦР7»·әН9»·Ј¬ФтРЎББХв8ҙОЙд»чіЙјЁөД·ҪІо Ј®ЈЁМоЎ°ұдҙуЎұЎўЎ°ұдРЎЎұЎўЎ°І»ұдЎұЈ©