题目内容
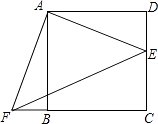
【题目】如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转△ABF的位置. 
(1)旋转中心是点 , 旋转角度是度;
(2)若连结EF,则△AEF是三角形;并证明;
(3)若四边形AECF的面积为25,DE=2,求AE的长.
【答案】
(1)A;90
(2)等腰直角
(3)解:由题意得:△ADE≌△ABF,
∴S四边形AECF=S正方形ABCD=25,
∴AD=5,而∠D=90°,DE=2,
∴ ![]() .
.
【解析】解:(1)如图,由题意得:
旋转中心是点A,旋转角度是90度.
所以答案是A、90.(2)由题意得:AF=AE,∠EAF=90°,
∴△AEF为等腰直角三角形.
所以答案是等腰直角.
【考点精析】解答此题的关键在于理解旋转的性质的相关知识,掌握①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目