题目内容
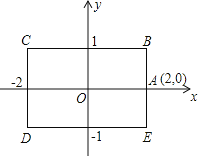
【题目】如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2012次相遇地点的坐标是【 】
A.(2,0) B.(-1,1) C.(-2,1) D.(-1,-1)
【答案】D。
【解析】利用行程问题中的相遇问题,由于矩形的边长为4和2,物体乙是物体甲的速度的2倍,求得每
一次相遇的地点,找出规律作答:
∵ 矩形的边长为4和2,物体乙是物体甲的速度的2倍,时间相同,
∴物体甲与物体乙的路程比为1:2。由题意知:
①第一次相遇物体甲与物体乙行的路程和为12×1,物体甲行的路程为12×![]() =4,物体乙行的路程为12×
=4,物体乙行的路程为12×![]() =8,在BC边相遇;
=8,在BC边相遇;
②第二次相遇物体甲与物体乙行的路程和为12×2,物体甲行的路程为12×2×![]() =8,物体乙行的路程为12×2×
=8,物体乙行的路程为12×2×![]() =16,在DE边相遇;
=16,在DE边相遇;
③第三次相遇物体甲与物体乙行的路程和为12×3,物体甲行的路程为12×3×![]() =12,物体乙行的路程为12×3×
=12,物体乙行的路程为12×3×![]() =24,在A点相遇;
=24,在A点相遇;
…
此时甲乙回到原出发点,则每相遇三次,两点回到出发点,
∵2012÷3=670…2,
故两个物体运动后的第2012次相遇地点的是:第二次相遇地点,即物体甲行的路程为12×2×![]() =8,物体乙行的路程为12×2×
=8,物体乙行的路程为12×2×![]() =16,在DE边相遇。
=16,在DE边相遇。
此时相遇点的坐标为:(-1,-1)。故选D。

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案【题目】某家电专卖店销售每台进价分别200元、160元的A,B两种型号的电风扇,下表是近两周的销售情况
销售时段 | 销售数量 | 销售收入 | |
A 种型号 | B种型号 | ||
第一周 | 3台 | 4台 | 1550 元 |
第二周 | 4台 | 8台 | 2600 元 |
(进价、售价均保持不变,利销=销售收入-进货成本)
(1)求A,B两种型号的电风扇的销售单价;
(2)若专卖店准备用不多于3560元的金额再采购这两种型号的电风扇共20台,且采购A型电风扇的数量不少于8台.求专卖店有哪几种采购方案?
(3)在(2)的条件下.如果采购的电风扇都能销售完,请直接写出哪种采购方案专卖店所获利润最大?最大利润是多少?




