题目内容
【题目】(本小题满分12分)
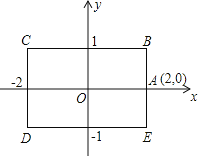
直线y=![]() x+6和x轴,y轴分别交于点E,F,点A是线段EF上一动点(不与点E重合),过点A作x轴垂线,垂足是点B,以AB为边向右作长方形ABCD,AB:BC=3:4.
x+6和x轴,y轴分别交于点E,F,点A是线段EF上一动点(不与点E重合),过点A作x轴垂线,垂足是点B,以AB为边向右作长方形ABCD,AB:BC=3:4.
(1)当点A与点F重合时(图1),求证:四边形ADBE是平行四边形,并求直线DE的表达式;
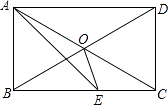
(2)当点A不与点F重合时(图2),四边形ADBE仍然是平行四边形?说明理由,此时你还能求出直线DE的表达式吗?若能,请你出来.

【答案】(1)![]() ;(2)四边形ADBE仍然是平行四边形;
;(2)四边形ADBE仍然是平行四边形;![]() .
.
【解析】
试题对于直线y=![]() x+6,分别令x与y为0求出y与x的值,确定出E与F坐标,
x+6,分别令x与y为0求出y与x的值,确定出E与F坐标,
(1)当A与F重合时,根据F坐标确定出A坐标,进而确定出AB的长,由AB与BC的比值求出BC的长,确定出AD=BE,而AD与BE平行,利用一组对边平行且相等的四边形为平行四边形得到四边形AEBD为平行四边形;根据AB与BC的长确定出D坐标,设直线DE解析式为y=kx+b,将D与E坐标代入求出k与b的值,即可确定出直线DE解析式;
(2)当点A不与点F重合时,四边形ADBE仍然是平行四边形,理由为:根据直线y=![]() x+6解析式设出A坐标,进而表示出AB的长,根据A与B横坐标相同确定出B坐标,进而表示出EB的长,发现EB=AD,而EB与AD平行,利用一组对边平行且相等的四边形为平行四边形得到四边形AEBD为平行四边形;根据BC的长求出OC的长,表示出D坐标,设直线DE解析式为y=k1x+b1,将D与E坐标代入求出k1与b1的值,即可确定出直线DE解析式.
x+6解析式设出A坐标,进而表示出AB的长,根据A与B横坐标相同确定出B坐标,进而表示出EB的长,发现EB=AD,而EB与AD平行,利用一组对边平行且相等的四边形为平行四边形得到四边形AEBD为平行四边形;根据BC的长求出OC的长,表示出D坐标,设直线DE解析式为y=k1x+b1,将D与E坐标代入求出k1与b1的值,即可确定出直线DE解析式.
试题解析:对于直线y=![]() x+6,
x+6,
令x=0,得到y=6;令y=0,得到x=﹣8,即E(﹣8,0),F(0,6),
(1)当点A与点F重合时,A(0,6),即AB=6,
∵AB:BC=3:4,
∴BC=8,
∴AD=BE=8,
又∵AD∥BE,
∴四边形ADBE是平行四边形;
∴D(8,6),
设直线DE解析式为y=kx+b(k、b为常数且k≠0),
将D(8,6),E(﹣8,0)代入得:![]() ,
,
解得:b=3,k=![]() .
.
则直线DE解析式为y=![]() x+3;
x+3;
(2)四边形ADBE仍然是平行四边形,理由为:
设点A(m,![]() m+6)即AB=
m+6)即AB=![]() m+6,OB=﹣m,即B(m,0),
m+6,OB=﹣m,即B(m,0),
∴BE=m+8,
又∵AB:BC=3:4,
∴BC=m+8,
∴AD=m+8,
∴BE=AD,
又∵BE∥AD,
∴四边形ADBE仍然是平行四边形;
又∵BC=m+8,
∴OC=2m+8,
∴D(2m+8,![]() m+6),
m+6),
设直线DE解析式为y=k1x+b1(k1、b1为常数且k1≠0),
将D与E坐标代入得: ,
,
解得:k1=![]() ,b1=3,
,b1=3,
则直线DE解析式为y=![]() x+3.
x+3.