��Ŀ����
����Ŀ������������һ�ַdz���Ҫ����ѧ���������һ�����ṩ����֪�����а���������������ǿ��Է������������⣮���磺��|x|=2��|y|=3��x+y��ֵ��
�������x=2��y=3ʱ��x+y=5
�������x=2��y=��3ʱ��x+y=��1
�������x=��2��y=3ʱ��x+y=1
�������x=��2��y=��3ʱ��x+y=��5
���ԣ�x+y��ֵΪ1����1��5����5��
���ε�ѧϰ������Ҳ�����Ƶ������
���⣨1������֪��A��B��C��һ��ֱ���ϣ���AB=8��BC=3����AC��Ϊ���٣�
ͨ���������Ƿ��֣�������������������
���������C�ڵ�B���Ҳ�ʱ����ͼ1����ʱ��AC=�� ��
���������C�ڵ�B�����ʱ����ͼ2����ʱ��AC=�� ��
ͨ���������⣬���Ƿ��֣�������ͼ���������Ǹ��õĽ��з��࣮
���⣨2������ͼ3�������ϵ�A�͵�B��ʾ�����ֱ��ǩ�1��2����C��������һ�㣬��BC=2AB�����C��ʾ�����Ƕ��٣�
��������1������ͼ�Σ����ͼ��д��������ͽ����
���⣨3������O��ֱ��AB��һ�㣬��OΪ�˵�������OC��OD��ʹ��AOC=60�㣬OCOD������BOD�Ķ���������ͼ�Σ�ֱ��д�������

���𰸡���1��11��5����2����C��ʾ����Ϊ��4��8����3������OC��OD��AB��ͬ��ʱ��30�㣻����OC��OD��AB�����ʱ��150��.
��������
��1������������������ۣ�������C�ڵ�B���Ҳ�ʱ��������C�ڵ�B�����ʱ���ֱ������߶εĺͲ��ϵ���м��㣻
��2������������������ۣ�������C�ڵ�B�����ʱ��������C�ڵ�B���Ҳ�ʱ���ֱ�����BC=2AB���м��㣻
��3������������������ۣ�����OC��OD��AB��ͬ��ʱ������OC��OD��AB�����ʱ���ֱ����ݽǵĺͲ��ϵ���м��㣮
�⣺��1�������������������֣�
������C�ڵ�B���Ҳ�ʱ����ͼ1����ʱ��AC=AB+BC=8+3=11��
������C�ڵ�B�����ʱ����ͼ2����ʱ��AC=AB��BC=8��3=5��
�ʴ�Ϊ��11��5��
��2�������������������֣�
������C�ڵ�B�����ʱ����ͼ����ʱ��BC=2AB=2��2+1��=6��
����C��ʾ����Ϊ2��6=��4��
![]()
������C�ڵ�B���Ҳ�ʱ����ͼ��BC=2AB=2��2+1��=6��
����C��ʾ����Ϊ2+6=8��
![]()
������������C��ʾ����Ϊ��4��8��
��3�������������������֣�
����OC��OD��AB��ͬ��ʱ����ͼ����BOD=180�㩁��AOC����COD=30�㣻
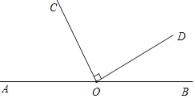
����OC��OD��AB�����ʱ����ͼ����BOD=180�㩁����COD����AOC��=150�㣻