题目内容
在平面直角坐标系中,已知点A(4,0)、B(﹣6,0),点C是y轴上的一个动点,当∠BCA=45°时,点C的坐标为 .
(0,12)或(0,﹣12)
试题分析:设线段BA的中点为E,
∵点A(4,0)、B(﹣6,0),∴AB=10,E(﹣1,0)。
(1)如答图1所示,过点E在第二象限作EP⊥BA,且EP=
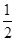 AB=5,
AB=5,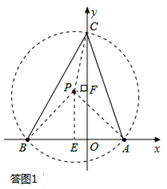
则易知△PBA为等腰直角三角形,∠BPA=90°,PA=PB=
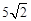 。
。以点P为圆心,PA(或PB)长为半径作⊙P,与y轴的正半轴交于点C,
∵∠BCA为⊙P的圆周角,
∴∠BCA=
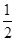 ∠BPA=45°,则点C即为所求。
∠BPA=45°,则点C即为所求。过点P作PF⊥y轴于点F,则OF=PE=5,PF=1,
在Rt△PFC中,PF=1,PC=
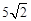 ,
,由勾股定理得:
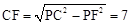 ,
,∴OC=OF+CF=5+7=12。
∴点C坐标为(0,12)。
(2)如答图2所示,根据圆满的对称性质,可得y轴负半轴上的点C坐标为(0,﹣12)。
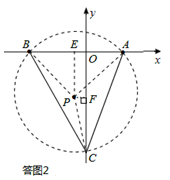
综上所述,点C坐标为(0,12)或(0,﹣12)。

练习册系列答案
相关题目
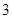 ,
, )关于原点对称的对称点的坐标是( )
)关于原点对称的对称点的坐标是( )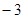 ,
,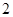 )
)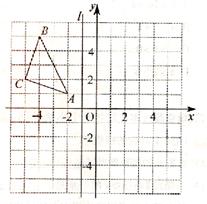

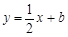 与△ABC有交点时,b的取值范围是( )
与△ABC有交点时,b的取值范围是( )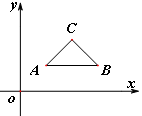
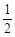 ≤
≤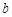 ≤1
≤1